
Newton's first law of motion specifies that when all the external forces on an object are balanced, there is no net external force and it will move at a constant velocity or remain at rest (velocity equals zero). This law holds for both linear motion and forces and for twisting motion and twisting forces. Twisting forces are called torques, or moments. The twisting motion occurs about some point called the pivot. A torque is related to a linear force; the torque about a point is equal to the force times the perpendicular distance to the point. In equilibrium, there are no net torques about the pivot and the angular velocity is constant (or zero).
Fundamentals
An excellent way for students to gain a feel for the action of torques and forces is to fly a kite. Kites can fly because of the forces acting on the parts of the kite. Though kites come in many shapes and sizes, the forces which act on a kite are the same for all kites. You can compare the forces to the forces acting on an airliner in flight and you will find that, with the exception of thrust, they are exactly the same. The similarity in forces allowed the Wright brothers to test their theories of flight by flying their aircraft as kites form 1900 to 1902.
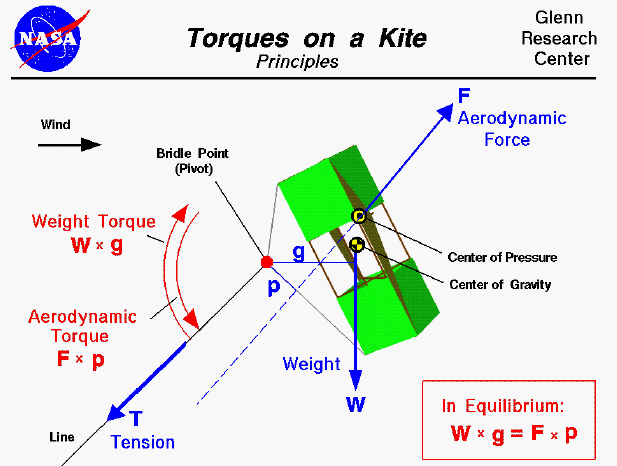
There are, however, some important differences in the response of a kite to external forces that do not occur in an airplane. An airplane in flight will rotate about its center of gravity. The center of gravity for any object is the average location of the weight of all the parts of the object. A kite in flight does not rotate about its center of gravity because it is pinned by the bridle to the control line. A kite in flight is more closely related to a hinged door than to an airplane in flight. The center of gravity of a hinged door is in the center of the door, but the door rotates about the hinges. A kite in flight rotates about the bridle point which is the place where the line is attached to the bridle as shown by the red dot on the slide.
There are three main forces which act on a kite; the weight, the aerodynamics, and the tension in the line. Because the bridle point is the pivot about which the kite rotates, the tension does not contribute to the torques on the system (the distance is zero). As shown on the figure, the weight produces a clockwise torque TW about the bridle point which is equal to the magnitude of the weight W times the perpendicular distance g from the bridle point to the center of gravity.
TW = W * g
The aerodynamic force produces a counterclockwise torque TF about the bridle point which is equal to the magnitude of the aerodynamic force F times the perpendicular distance p from the bridle point to the center of pressure.
TF = F * p
Notice that the distances are measured perpendicular to the forces and not just directly to the center of pressure and center of gravity.
In equilibrium, these torques are balanced and there is no rotation of the kite about the bridle point. This is called a trimmed flight condition.
W * g = F * p
The Tricky Part
In flight, a kite can rotate about the bridle point. As the kite rotates, the inclination angle between the kite and the wind changes. The magnitude and direction of the aerodynamic force depends on this angle and the ratio of the lift and drag which depends on the design of the kite. So as the kite rotates, the aerodynamic force changes and this changes the aerodynamic torque about the bridle point as discussed above. If the changing aerodynamic torque balances the weight torque, the kite reaches an equilibrium condition and sits at a fixed inclination angle with no further rotation about the bridle point. But if the aerodynamic torque does not equal the weight torque, the kite continues to rotate under the action of the unequal torques. It is possible that the aerodynamic torque never equals the weight torque which causes the kite to continually rotate.
In equilibrium the kite is inclined to the wind (and to the ground) at a fixed angle and the magnitude of the lift force depends directly on this angle. Since the weight of the kite is constant, the difference between the lift and the weight is an indication of how well the kite will fly. If the lift is greater, the kite will climb faster, fly higher, and is able to lift more string. If the lift is less, the kite will climb slowly or maybe not at all! Since the flight angle depends on the balance of torques, and the torques depend on the location of the bridle point relative to the cg and cp, the location of the bridle point has a major effect on the performance of the kite. The location of the bridle point can be changed by the flyer before launch.
The mathematical equations involved with the forces and torques on a kite can be solved by using a computer program. You can use the KiteModeler program to further study how kites work and to design your own kites.
Navigation...
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov