
An excellent way to gain an understanding and a feel for aerodynamic forces is to fly a kite. Kite flying is fun when done safely and you can study many of the fundamentals of airplane aerodynamics because a kite works very much like an airplane. As with an airplane, there are some geometrical definitions which will simplify our studies of kite aerodynamics. Kites come a wide variety of shapes and sizes, but the definitions found on this page can be applied to most kites.
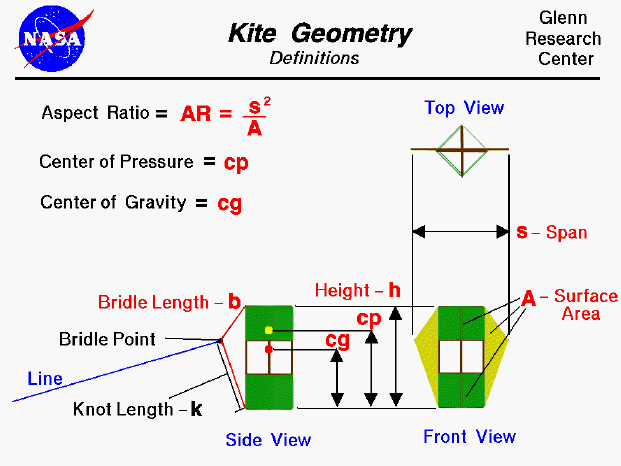
This page shows a three view diagram of a winged box kite. In a three view diagram, an object is shown from the front, side, and top with all three views drawn to the same scale. We use three view diagrams because some geometrical variables are easier to visualize in one view than in another.
Beginning with the Front View, we note that the surface area-A which is used in the calculation of lift and drag is the frontal projected area of all of the surfaces of the kite. (You learn how to compute the area of various shaped objects in middle school). For this winged box kite, this would include the full area of both wings (colored yellow) and the projected area of the top and bottom boxes (colored green). Notice that this is a "projected" area, not a geometric area. If each panel of the box kite is a square, there are four panels on the top and four on the bottom to form the two boxes. From the Top View, we see that each panel is inclined to the front at a 45 degree angle. Then the projected area of each panel is equal to the geometric area times the cosine of 45 degrees (.707). The top and front view also help us define the span-s of the kite. The span is the widest distance from side to side. It is the same as the wing span of an airplane, the distance from one wing tip to the other wing tip. The ratio of the square of the span to the area is called the Aspect Ratio of the kite. This parameter is very important in the determination of lift and drag of the kite. Airplane wings typically have a very long span and have a high aspect ratio. Kites on the other hand usually have a small span and are low aspect ratio aircraft.
The Side View helps us locate the center of gravity-cg and the center of pressure-cp of the kite. The center of gravity is the average location of the weight of the kite, and the weight force acts through this point. Similarly, the center of pressure is the average location of the aerodynamic forces on the kite, and the lift and drag act through this point. There are techniques to determine the weight, cg, and cp which are described on separate pages. On the front of the kite (to the left in this side view) we attach a bridle string. The bridle length-b is the length of the string from one end attached to the top to the other end attached to the bottom of our kite. It is always longer than the height-h of the kite, so there is some slack in this string. A knot is used to attach the control line to the bridle at a spot called the bridle point. The knot length-k is the distance from the bottom to the knot along the bridle string. The knot length and the bridle length determine the location of the bridle point. In flight, the kite rotates about the bridle point. A kite's stability is determined by the magnitude of the forces and the distance of the cg and cp from the bridle point.
The KiteModeler computer program can be used to calculate the various geometric variables described on this page and their effects on kite performance.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov