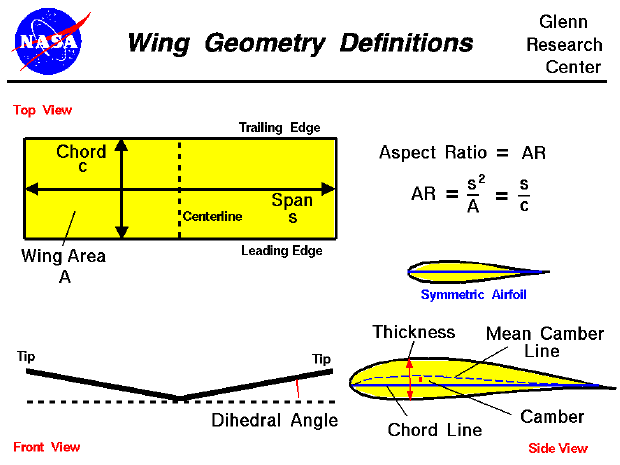

This slide gives technical definitions of a wing's geometry, which is one of the chief factors affecting airplane lift and drag. The terminology is used throughout the airplane industry and is also found in the FoilSim program developed here at NASA Glenn. Actual aircraft wings are complex three-dimensional objects, but we will start with some simple definitions. The figure shows the wing viewed from three directions; the upper left shows the view from the top looking down on the wing, the lower left shows the view from the front looking at the wing leading edge, and the right shows a side view from the left looking in towards the centerline. The side view shows an airfoil shape with the leading edge to the left.
Top View
The top view shows a simple wing geometry, like that found on a light general aviation aircraft. The front of the wing (at the bottom) is called the leading edge; the back of the wing (at the top) is called the trailing edge. The distance from the leading to trailing edges is called the chord, denoted by the symbol c. The ends of the wing are called the wing tips, and the distance from one wing tip to the other is called the span, given the symbol s. The shape of the wing, when viewed from above looking down onto the wing, is called a planform. In this figure, the planform is a rectangle. For a rectangular wing, the chord length at every location along the span is the same. For most other planforms, the chord length varies along the span. The wing area, A, is the projected area of the planform and is bounded by the leading and trailing edges and the wing tips. Note: The wing area is NOT the total surface area of the wing. The total surface area includes both upper and lower surfaces. The wing area is a projected area and is almost half of the total surface area.
Aspect ratio is a measure of how long and slender a wing is from tip to tip. The Aspect Ratio of a wing is defined to be the square of the span divided by the wing area and is given the symbol AR. For a rectangular wing, this reduces to the ratio of the span to the chord length as shown at the upper right of the figure.
AR = s^2 / A = s^2 / (s * c) = s / c
High aspect ratio wings have long spans (like high performance gliders), while low aspect ratio wings have either short spans or thick chords (like the Space Shuttle). There is a component of the drag of an aircraft called induced drag which depends inversely on the aspect ratio. A higher aspect ratio wing has a lower drag and a slightly higher lift than a lower aspect ratio wing. Because the glide angle of a glider depends on the ratio of the lift to the drag, a glider is usually designed with a very high aspect ratio. The Space Shuttle has a low aspect ratio because of high speed effects, and therefore is a very poor glider. The F-14 and F-111 have the best of both worlds. They can change the aspect ratio in flight by pivoting the wings--large span for low speed, small span for high speed.
Front View
The front view of this wing shows that the left and right wing do not lie in the same plane but meet at an angle. The angle that the wing makes with the local horizontal is called the dihedral angle. Dihedral is added to the wings for roll stability; a wing with some dihedral will naturally return to its original position if it encounters a slight roll displacement. You may have noticed that most large airliner wings are designed with diherdral. The wing tips are farther off the ground than the wing root. Highly maneuverable fighter planes, on the other hand do not have dihedral. In fact, some fighter aircraft have the wing tips lower than the roots giving the aircraft a high roll rate. A negative dihedral angle is called anhedral . Historical Note: The Wright brothers designed their 1903 flyer with a slight anhedral to improve the aircraft roll performance.
Side View
A cut through the wing perpendicular to the leading and trailing edges will show the cross-section of the wing. This side view is called an airfoil, and it has some geometry definitions of its own as shown at the lower right. The straight line drawn from the leading to trailing edges of the airfoil is called the chord line. The chord line cuts the airfoil into an upper surface and a lower surface. If we plot the points that lie halfway between the upper and lower surfaces, we obtain a curve called the mean camber line. For a symmetric airfoil (upper surface the same shape as the lower surface) the mean camber line will fall on top of the chord line. But in most cases, these are two separate lines. The maximum distance between the two lines is called the camber, which is a measure of the curvature of the airfoil (high camber means high curvature). The maximum distance between the upper and lower surfaces is called the thickness. Often you will see these values divided by the chord length to produce a non-dimensional or "percent" type of number. Airfoils can come with all kinds of combinations of camber and thickness distributions. NACA (the precursor of NASA) established a method of designating classes of airfoils and then wind tunnel tested the airfoils to provide lift coefficients and drag coefficients for designers.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov