
An excellent way to gain an understanding and a feel for the interaction of forces on an object is to fly a kite. Kite flying is fun when done safely and you can study many of the fundamentals of airplane aerodynamics because a kite works very much like an airplane. There are, however, some important differences in the response of a kite to external forces that do not occur in an airplane. An airplane in flight rotates about its center of gravity which is the average location of the weight of all the parts of the airplane. A kite in flight does not rotate about its center of gravity because it is pinned by the bridle to the control line. In flight, the kite rotates about the bridle point which is the place where the line is attached to the bridle. (A kite in flight is more closely related to a hinged door than to an airplane in flight. The center of gravity of a hinged door is in the center of the door, but the door rotates about the hinges.)
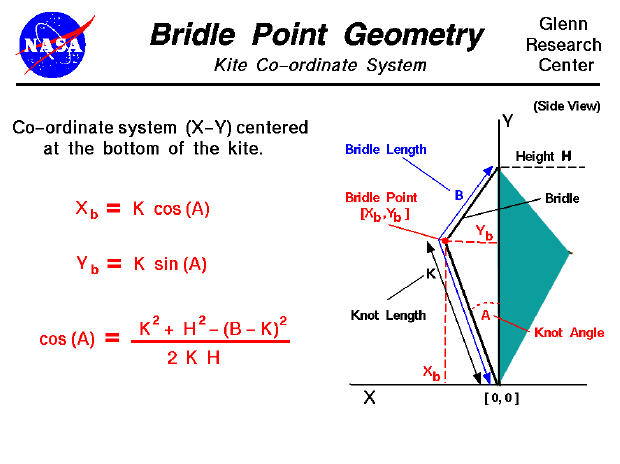
The location of the bridle point relative to the center of gravity (cg) and center of pressure (cp) determines the balance of torques on the kite and the trim angle at which the kite flies. On this page we show how to compute the location of the bridle point. We have an installed an X-Y co-ordinate system on the kite with the origin at the bottom of the kite; the Y-axis is along the height H of the kite, the X-axis is perpendicular to the Y-axis and goes through the bottom of the kite. The X-axis is used as the reference line in the computation of cg and cp. The length of the bridle is called B and is measured from the origin to the top of the kite along the bridle string. The bridle is attached to the control line with a knot. The distance from the knot to the origin is length K. The knot (bridle point) is inclined at an angle to Y-axis which is called the knot angle A. The co-ordinates of the bridle point are Xb and Yb and from trigonometry:
Xb = K * cos(A)
Yb = K * sin(A)
To determine the angle A, we need another formula from trigonometry. This formula relates the sides and angles of any general triangle. We will apply the formula to the triangle formed by the bridle and the height of the kite.
cos(A) = [K^2 + H^2 - (B - K)^2] / (2 * K * H)
The KiteModeler computer program can be used to calculate the various geometric variables described on this page and their effects on kite performance.
Navigation...
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov