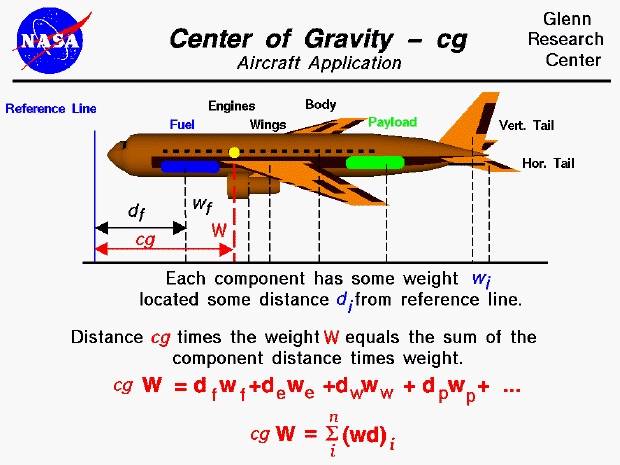

An airplane in flight can be maneuvered by the pilot using the aerodynamic control surfaces, the elevator, rudder, or ailerons. As the control surfaces change the amount of force that each surface generates, the aircraft will rotate about a point called the center of gravity. The center of gravity is the average location of the weight of the aircraft. The mass (and weight) is actually distributed throughout the airplane, and for some problems it is important to know the distribution. But for total aircraft maneuvering, we need to be concerned with only the total weight and the location of the center of gravity.
How do engineers determine the location of the center of gravity for an airplane which they are designing?
In general, determining the center of gravity is a complicated procedure requiring the use of calculus as discussed on another page. The figure shown above is a simplified version that can be used by secondary students. For this figure, we assume that we already know the weight and location, relative to some reference location, of each of the major components of the airplane (the fuselage, vertical and horizontal tails, wings, engines, fuel, payload, etc.). The total weight of the aircraft is simply the sum of all the individual weights of the components. Since the center of gravity is an average location of the weight, we can say that the weight of the entire aircraft times the location of the center of gravity is equal to the sum of the weight of each component times the distance of that component from the reference location. (To simplify: the center of gravity is the mass-weighted average of the component locations.)
For each of the components, the center of gravity is the average distance of the weight from some reference line. If we have a solid block of uniform material, the calculation is simply the average of physical dimensions. (If we have a rectangular block, 50 X 20 X 10, the center of gravity is at the point (25,10, 5) ). But if the block is nonuniform in either its density or its shape, we have to resort to more sophisticated averaging techniques. We can generalize the technique discussed above. If we had a total of "n" discrete components, the center of gravity (cg) of the aircraft times the weight (W) of the aircraft would be the sum of the individual (i) component weight times the distance from the reference line (wd) with the index i going from 1 to n. Mathematicians use the greek letter sigma to denote this addition. (Sigma is a zig-zag symbol with the index designation being placed below the bottom bar, the total number of additions placed over the top bar, and the variable to be summed placed to the right of the sigma with each component designated by the index.) So this equation says that the center of gravity times the sum of "n" parts' weight is equal to the sum of "n" parts' weight times their distance. The discrete equation works for "n" discrete parts.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov