The center of gravity is a geometric property of any object. The center of gravity is the average location of the weight of an object. We can completely describe the motion of any object through space in terms of the translation of the center of gravity of the object from one place to another, and the rotation of the object about its center of gravity if it is free to rotate. If the object is confined to rotate about some other point, like a hinge, we can still describe its motion. In flight, both airplanes and rockets rotate about their centers of gravity. A kite, on the other hand, rotates about the bridle point. But the trim of a kite still depends on the location of the center of gravity relative to the bridle point, because for every object the weight always acts through the center of gravity.

Determining the center of gravity is very important for any flying object. How do engineers determine the location of the center of gravity for an aircraft which they are designing?

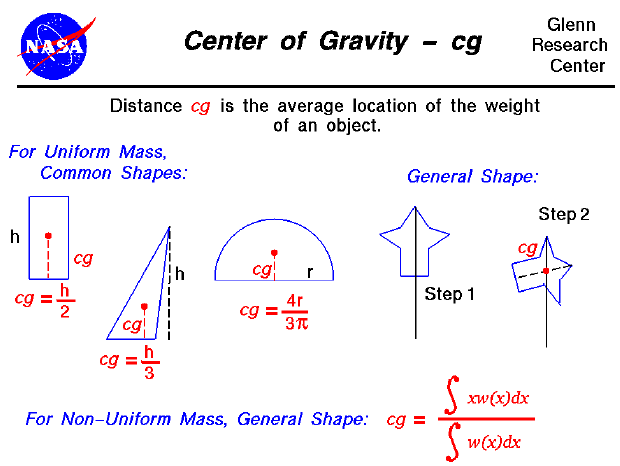
In general, determining the center of gravity (cg) is a complicated procedure because the mass (and weight) may not be uniformly distributed throughout the object. The general case requires the use of calculus which we will discuss at the bottom of this page. If the mass is uniformly distributed, the problem is greatly simplified. If the object has a line (or plane) of symmetry, the cg lies on the line of symmetry. For a solid block of uniform material, the center of gravity is simply at the average location of the physical dimensions. (For a rectangular block, 50 X 20 X 10, the center of gravity is at the point (25,10, 5) ). For a triangle of height h, the cg is at h/3, and for a semi-circle of radius r, the cg is at (4*r/(3*pi)) where pi is ratio of the circumference of the circle to the diameter. There are tables of the location of the center of gravity for many simple shapes in math and science books. The tables were generated by using the equation from calculus shown on the slide.

For a general shaped object, there is a simple mechanical way to determine the center of gravity:

1. If we just balance the object using a string or an edge, the point at which the object is balanced is the center of gravity. (Just like balancing a pencil on your finger!)
2. Another, more complicated way, is a two step method shown on the slide. In Step 1, you hang the object from any point and you drop a weighted string from the same point. Draw a line on the object along the string. For Step 2, repeat the procedure from another point on the object You now have two lines drawn on the object which intersect. The center of gravity is the point where the lines intersect. This procedure works well for irregularly shaped objects that are hard to balance.

If the mass of the object is not uniformly distributed, we can characterize the mass distribution by a function w(x) which indicates that the weight is some function of distance x from a reference line. If we can determine the form of the function, there are methods to perform a calculus integration of the equation. We will use the symbols "S[ ]dx" to denote the integration of a continuous function. Then the center of gravity can be determined from:

If we don't know the actual functional form, we can numerically integrate the equation using a spreadsheet by dividing the distance into a number of small distance segments and determining the average value of the mass (or weight) over that small segment. Taking the sum of the average value times the distance times the distance segment divided by the sum of the average value times the distance segment will produce the center of gravity.

• Aircraft Weight:
• Fuselage:

Navigation..

Beginner's Guide to Aerodynamics

Beginner's Guide to Propulsion

Beginner's Guide to Model Rockets

Beginner's Guide to Kites

Beginner's Guide to Aeronautics

Back to top

Go to...

Beginner's Guide Home Page

byTom Benson
Please send suggestions/corrections to: benson@grc.nasa.gov