
The flight characteristics of a kite depend on the relative size of the forces which act on the kite and where those forces act on the kite. The forces include the aerodynamic lift, and drag which act through the center of pressure, the tension in the control line which acts through the bridle point, and the weight which acts through the center of gravity. We can predict the performance of a kite design if we can calculate all of these forces and locations.
The center of gravity is the average location of the weight of the kite. To determine the stability and trim of the kite we need to be concerned with the total weight and the location of the center of gravity because the weight acts through the center of gravity. How would you determine the location of the center of gravity during design?
Calculating cg
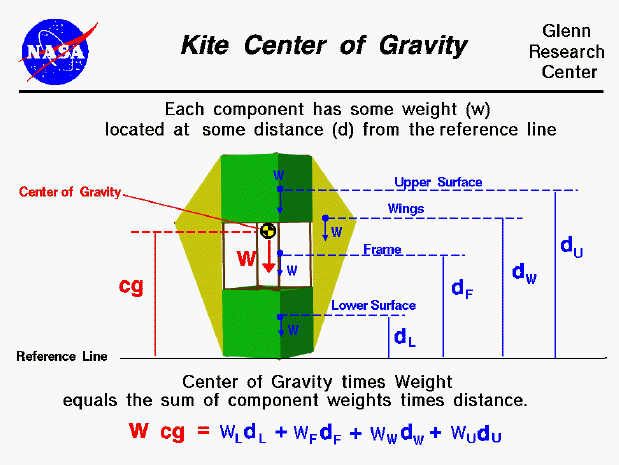
You can calculate the center of gravity. But in general, this is a complicated procedure requiring the use of calculus. This figure shows a simplified version of the center of gravity calculation that you can use. We assume that we already know the weight and location, relative to some reference location, of each of the major parts of the kite including the frame and the surface covering. The total weight (W) of the kite is simply the sum of the weight of the surface covering and the frame. Since the center of gravity (cg) is an average location of the weight, we can say that the weight of the whole kite times the location of the center of gravity is equal to the sum of the weight of each part times the distance of that part from the reference location. (This is equivalent to saying the center of gravity is the mass-weighted average of the part locations.) On this page we show a winged box kite and the parts include the upper surface, the lower surface, both wings and the frame. For a different design the number and location of the parts would be different. For the winged box kite, the weight times the center of gravity is equal to the weight of the upper surface times the distance of the upper surface, plus the weight of lower surface times the distance to the lower surface plus the weight of the frame times the distance to the frame plus the weight of the wings times the distance to the wing:
W * cg = (w * d)u + (w * d)l + (w * d)f + (w * d)w
You can use the KiteModeler computer program to calculate values for the center of gravity of your design. Select "Design" mode and change the geometry of your kite using input sliders. The program calculates the center of gravity using the equation listed above and displays the output results.
Component cg Location
On the page, we show the weight and distance of the parts relative to the reference line. The location of the reference line is arbitrary (it could be measured from the top of the kite instead of from the base of the kite as shown in the figure) but we have to remember where it is. The cg is a distance measured from the reference line as well. The "distance" of the upper surface (du) is the distance of the center of gravity of the upper surface relative to the reference line. So we have to be able to calculate or determine the center of gravity of the upper surface and each of the other kite parts. For simple shapes, finding the cg, or average location of the weight, is quite simple. For example, the upper surface is a rectangle. The center of gravity is halfway between the top and bottom of the upper surface. For a triangle it is 1/3 of the distance from the side. There is a technique for determining the center of gravity of any general shape, and the details of this technique is given on another page.
Determining cg Mechanically
Once we have built a kite, there is a simple mechanical way to determine the center of gravity for each component or for the entire kite:
Navigation...
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov