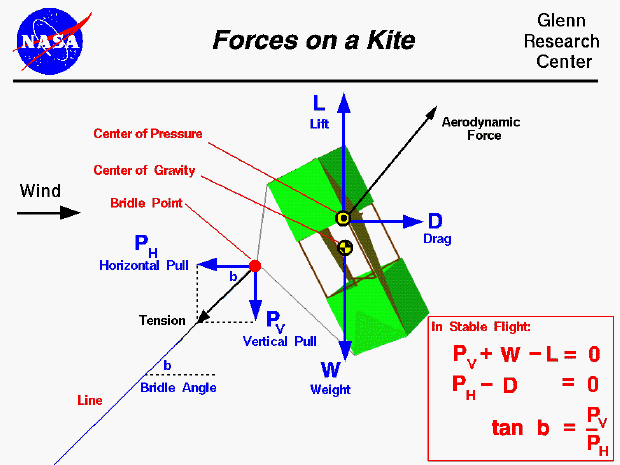

An excellent way for students to gain a feel for aerodynamic forces is to fly a kite. Kites can fly because of the forces acting on the parts of the kite. Though kites come in many shapes and sizes, the forces which act on a kite are the same for all kites and are shown on this slide. You can compare these forces to the forces acting on an airliner in flight and you will find that, with the exception of thrust, they are exactly the same. The similarity in forces allowed the Wright brothers to test their theories of flight by flying their aircraft as kites from 1900 to 1902.
This page shows a free body diagram of the kite. In a free body diagram, we draw a single object and all of the forces which act on that object. Forces are vectors having both a magnitude and a direction, so we draw each force as an arrow with the length proportional to the magnitude and the head of the arrow pointing in the direction of the force. An important property of vectors is that they can be broken down into perpendicular components, and we can develop scalar equations in each component direction.
On the page, there are three principle forces acting on the kite; the weight, the tension in the line, and the aerodynamic force. The weight W always acts from the center of gravity toward the center of the earth. The aerodynamic force is usually broken into two components (shown in blue); the lift L, which acts perpendicular to the wind, and the drag D, which acts in the direction of the wind. The aerodynamic force acts through the center of pressure. Near the ground, the wind may swirl and gust because of turbulence in the earth's boundary layer. But away from the ground, the wind is fairly constant and parallel to the surface of the earth. In this case, the lift is directly opposed to the weight of the kite, as shown in the figure. The tension in the line acts through the bridle point where the line is attached to the kite bridle. We break the tension into two components, the vertical pull Pv, and the horizontal pull Ph.
When the kite is in stable flight the forces remain constant and there is no net external force acting on the kite, from Newton's first law of motion. In the vertical direction, the sum of the forces is zero. So, the vertical pull plus the weight minus the lift is equal to zero.
Pv + W - L = 0
In the horizontal direction, the sum of the horizontal pull and the drag must also equal zero.
Ph - D = 0
With some knowledge of the kite geometry and the velocity of the wind, we can determine the value of the lift and drag. And with knowledge of the kite geometry and the materials used to make the kite we can determine the weight. We can then solve the two equations given above for the horizontal and vertical components of the tension in the line.
Near the bridle point, the line is inclined at an angle called the bridle angle b. The magnitude of this angle is related to the relative magnitude of the components of the tension.
tan b = Pv / Ph
Knowing the bridle angle, the length of line, and the weight per length of line, you can predict the height at which the kite is flying. You can use the KiteModeler program to solve all the equations shown on this slide.
The relative strength of the forces determines the motion of the kite as described by Newton's laws of motion. If a gust of wind strikes the kite, the lift and drag increase. The kite then moves vertically because the lift now exceeds the weight and the vertical pull, and the tension force increases because of increased drag. Eventually a new balance point is established and the kite achieves a different stable condition. Because of the change in relative strength of the aerodynamic and weight forces, the kite also rotates about the bridle point to balance the torques.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov