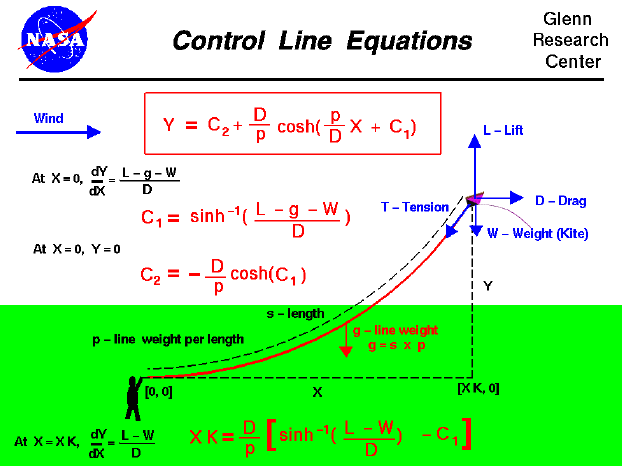

An excellent way for students to gain a feel for aerodynamic forces is to fly a kite. The motion of the kite through the air is the result of forces being applied to the kite. The kite responds to these forces according to Newton's laws of motion. When the kite is in cruising flight you will notice that the control line produces a gentle curve from the hand of the flyer to the kite; the line sags under its own weight.
Mathematical equations have been developed which describe the shape of the control line and we will now discuss these equations. A co-ordinate system has been established with the X axis along the ground, the Y axis perpendicular to the ground; the origin is the hand of the kite flyer. The kite is subjected to four main forces; the lift L, the drag D, the weight W, and the tension T in the control line. The control line has a certain length s and the weight of the control line is evenly distributed along the length at p ounces per foot of line. The total weight of the control line is designated g and
g = s * p
Because the weight of the control line is evenly distributed along the length, the line hangs under its own weight. A differential equation describes the transmission of the forces along the control line. (The math involved in the derivation and solution of this equation is taught in second year calculus classes.) Solving the differential equation, we can relate the shape of the control line (Y versus X) to the distribution of the tension in the control line. The resulting equation is shown in the red box at the top of the page.
Y = C2 + (D/p) * cosh [(p/D) * X + C1]
C1 and C2 are called constants of integration and must be determined at the boundaries of the problem. The symbol cosh indicates the hyperbolic cosine function. This is just a tabulated function, like the trigonometric cosine, sine, and tangent, but with different values for a given input. There is also a hyperbolic sine, sinh, and a hyperbolic tangent, tanh, which we won't need for this problem. The equation in the red box is called a Catenary and was developed many years ago to describe cables hanging under their own weight. Other examples would include telephone wires, cables on a suspension bridge, and even a jump rope!
To solve for C1 and C2 we first use the boundary condition that at X=0, Y=0. Plugging X=0 into the catenary equation gives a relationship between the two constants
C2 = -(D/p) * cosh (C1)
So if we can determine C1, we now know C2. To get C1 we note that at the origin (X=0) the slope of the control line (dY/dX) is equal to the ratio of the component forces.
At X=0, dY/dX = (L - g - W) / D
The derivative of the cosh is the sinh. Plugging in X=0 gives the equation:
C1 = sinh^-1[(L - g - W) / D ]
where sinh^-1 indicates the inverse hyperbolic sine of the expression. That just means that the sinh(C1) is equal to (L - g - W) / D. There are also tables of inverse hyperbolic sines, just like there are tables of inverse sines in trigonometry. With this value of C1 and the other equation to get C2 as a function of C1, we now know the equation of the entire length of the control line.
The kite flies at some distance XK downwind from the flyer. At the kite we know that the slope of the control line is given by:At X=XK, dY/dX = (L - W) / D
We can use this information to determine the length XK for a given length of string s. This equation is given at the bottom:
XK = (D / p) * [sinh^-1((L - W) / D) - C1]
The dependence on s is hidden in the constant C1. We could instead write:
XK = (D / p) * [sinh^-1((L - W) / D) - sinh^-1((L - W - p*s)/D)]
If we then plug this value of XK into the catenary equation, we can solve for the height Y at which the kite is flying above the ground. Notice that the shape of the line is not a straight line, so we can not use trigonometry to get the height for a given length of line.
These mathematical equations are pretty messy! So we have written a computer program to solve them for you. You can use the KiteModeler computer program to solve these equations for a kite which you can design. You can then build your own kite from your design and compare the actual flight performance to this computer prediction. You can determine the altitude at which you kite actually flies by using some simple math techniques and a little graph paper. With a little more mathematical knowledge you can even calculate the altitude at which the kite is flying.Enjoy flying ... but always fly safely.
Navigation...
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov