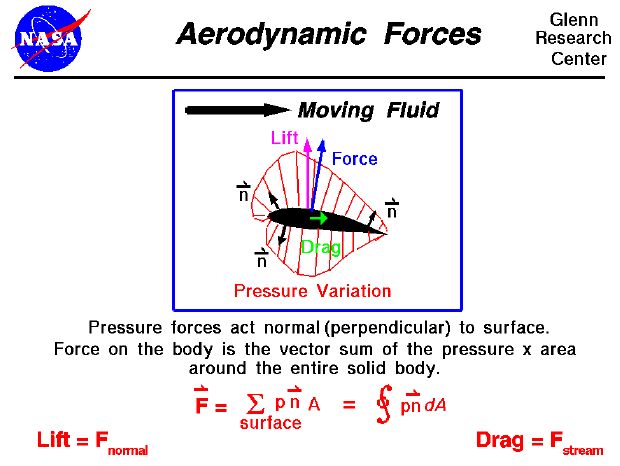

When two solid objects interact in a mechanical process, forces are transmitted, or applied, at the point of contact. But when a solid object interacts with a fluid, things are more difficult to describe because the fluid can change its shape. For a solid body immersed in a fluid, the "point of contact" is every point on the surface of the body. The fluid can flow around the body and maintain physical contact at all points. The transmission, or application, of mechanical forces between a solid body and a fluid occurs at every point on the surface of the body. And the transmission occurs through the fluid pressure.
Variation in Pressure
The magnitude of the force acting over a small section of an object equals the pressure times the area of the section. A quick units check shows that pressure (force/area) times area produces a force. As discussed on the fluid pressure slide, pressure is a scalar quantity related to the momentum of the molecules of a fluid. Since a force is a vector quantity, having both magnitude and direction, we must determine the direction of the force. Pressure acts perpendicular (or normal) to the solid surface of an object. So the direction of the force on the small section of the object is along the normal to the surface. We denote this direction by the letter n.
The normal direction
changes from the front of the airfoil to the rear and from the top to
the bottom. To obtain the net mechanical force over the entire solid
object, we must sum the contributions from all the small sections.
Mathematically, the summation is indicated by the Greek letter
sigma (![]() )
The aerodynamic force F is equal to the sum of the product of
the pressure p times the area A in the normal direction.
)
The aerodynamic force F is equal to the sum of the product of
the pressure p times the area A in the normal direction.
F = ![]() p * A * n
p * A * n
In the limit of infinitely small sections, this gives the integral of the pressure times the area around the closed surface. If the pressure on a closed surface is a constant, there is no net force produced because the summation of the directions of the normal adds up to zero. (For every small section there is another small section whose normal points in exactly the opposite direction.)
Definitions of Lift and Drag
For a fluid in motion, the velocity will have different values at different locations around the body. The local pressure is related to the local velocity, so the pressure will also vary around the closed surface and a net force is produced. Summing (or integrating) the pressure perpendicular to the surface times the area around the body produces a net force. Since the fluid is in motion, we can define a flow direction along the motion. The component of the net force perpendicular (or normal) to the flow direction is called the lift; the component of the net force along the flow direction is called the drag. These are definitions. In reality, there is a single, net, integrated force caused by the pressure variations along a body. This aerodynamic force acts through the average location of the pressure variation which is called the center of pressure.
Velocity Distribution
For an ideal fluid with no boundary layers, the surface of an object is a streamline. If the velocity is low, and no energy is added to the flow, we can use Bernoulli's equation along a streamline to determine the pressure distribution for a known velocity distribution. If boundary layers are present, things are a little more confusing, since the external flow responds to the edge of the boundary layer and the pressure on the surface is imposed from the edge of the boundary layer. If the boundary layer separates from the surface, it gets even more confusing. How do we determine the velocity distribution around a body? Specifying the velocity is the source of error in two of the more popular incorrect theories of lift. To correctly determine the velocity distribution, we have to solve equations expressing a conservation of mass, momentum, and energy for the fluid passing the object.
Summary
So, to summarize, for any object immersed in a fluid, the mechanical forces are transmitted at every point on the surface of the body. The forces are transmitted through the pressure, which acts perpendicular to the surface. The net force can be found by integrating (or summing) the pressure times the area around the entire surface. For a moving flow, the pressure will vary from point to point because the velocity varies from point to point. For some simple flow problems, we can determine the pressure distribution (and the net force) if we know the velocity distribution by using Bernoulli's equation.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov