
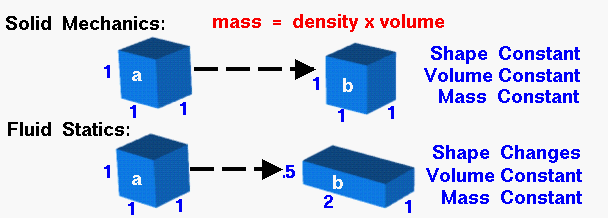



Solid Mechanics
The conservation of mass is a fundamental concept of physics along with the conservation of energy and the conservation of momentum. Within some problem domain, the amount of mass remains constant--mass is neither created nor destroyed. This seems quite obvious, as long as we are not talking about black holes or very exotic physics problems. The mass of any object can be determined by multiplying the volume of the object by the density of the object. When we move a solid object, as shown at the top of the slide, the object retains its shape, density, and volume. The mass of the object, therefore, remains a constant between state "a" and state "b."
Fluid Statics
In the center of the figure, we consider an amount of a static fluid (liquid or gas). If we change the fluid from some state "a" to another state "b" and allow it to come to rest, we find that, unlike a solid, a fluid may change its shape. The amount of fluid, however, remains the same. We can calculate the amount of fluid by multiplying the density times the volume. Since the mass remains constant, the product of the density and volume also remains constant. (If the density remains constant, the volume also remains constant.) The shape can change, but the mass remains the same.
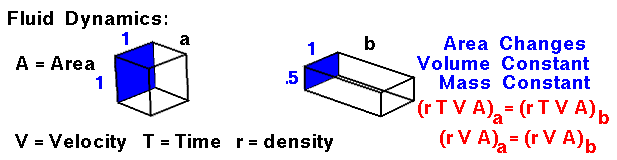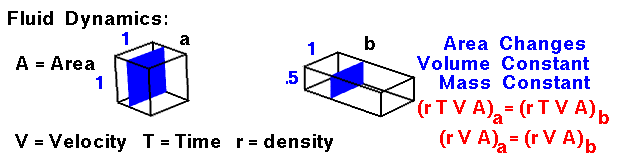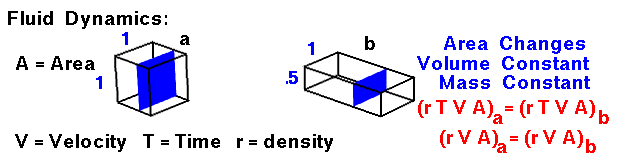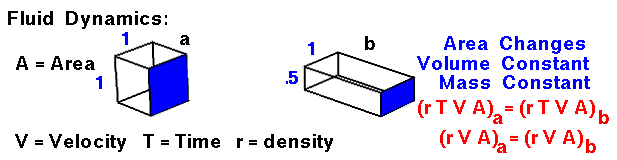
Fluid Dynamics
Finally, at the bottom of the slide, we consider the changes for a fluid that is moving through our domain. There is no accumulation or depletion of mass, so mass is conserved within the domain. Since the fluid is moving, defining the amount of mass gets a little tricky. Let's consider an amount of fluid that passes through point "a" of our domain in some amount of time (T). If the fluid passes through an area (A) at velocity (V), we can define the volume to be A times V, times T. (A units check gives area x length/time x time = area x length = volume). Thus the mass is simply density times A, times V, times T. If we compare the flow through another point in the domain, point "b," for the same amount of time (T), we find the mass to be the density times the velocity at "b," times the area of "b." Since the times are the same, we can eliminate the time dependence. The resulting equation is: r * V * A = constant.
The conservation of mass gives us an easy way to determine the velocity of flow in a tube if the density is constant. If we can determine (or set) the velocity at some known area, the equation tells us the value of velocity for any other area. In our animation, the area of "b" is one half the area of "a." Therefore, the velocity at "b" must be twice the velocity at "a." If we desire a certain velocity in a tube, we can determine the area necessary to obtain that velocity. This information is used in the design of wind tunnels. The quantity (density times area, times velocity) has the dimensions of mass/time and is called the mass flow rate. This quantity appears in our derivation of the momentum effects on lift and is an important parameter in determining the thrust produced by a propulsion system.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov