
An excellent way for students to gain a feel for aerodynamic forces is to fly a kite. Kites can fly because of forces acting on the parts of the kite. Though kites come in many shapes and sizes, the forces which act on the kite are the same for all kites. You can compare these forces to the forces that act on an airliner in flight and you will find that, with the exception of thrust, they are exactly the same. The similarity in forces allowed the Wright brothers to test their theories of flight by flying their aircraft as kites from 1900 to 1902.
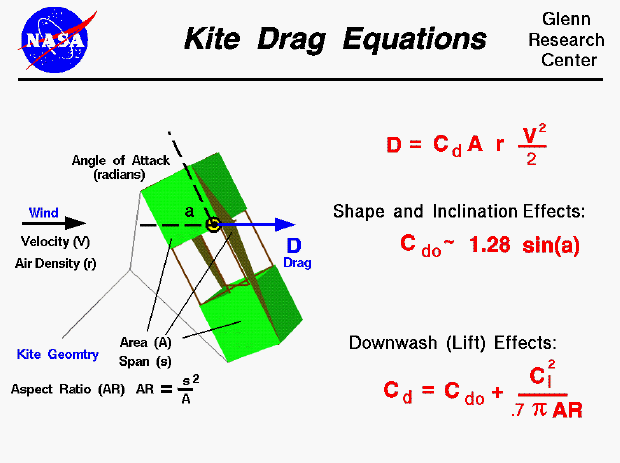
On this slide we show the equations which would describe the drag of a flying kite. The graphic shows a side view of the flying kite with the aerodynamic drag shown by the blue vector. The wind is blowing parallel to the ground and the drag is aligned with the wind.
Since the forces on a kite are the same as the forces on an airplane, we can use the mathematical equations developed to predict airplane performance to predict the aerodynamic performance of a kite. In particular, the drag equation shown on the upper right side of the has been developed for aircraft. The drag D is equal to a drag coefficient Cd times the projected surface area A times the air density r times one half the square of the wind velocity V.
D = Cd * A * r * .5 * V^2
The drag depends on two properties of the air; the density and velocity. In general, the density depends on your location on the earth. The higher the elevation, the lower the density. The standard value for air density at sea level conditions is 1.229 kg/m^3 or .00237 slug/ft^3. The variation of air density with altitude is described on a separate page. The air velocity is the relative speed between the kite and the air. When the kite is held fixed by the control line, the air velocity is the wind speed. If the line breaks, or if you let out line, the velocity is something less than the wind speed; if you pull on the control line the velocity is the wind speed plus the speed of your pull. The drag changes with the square of the velocity as described on another page.
The aerodynamic drag on your kite depend directly on the surface area of the kite. You first learn how to compute the area for a geometric shape while you are in middle school. The surface area depends on the particular design of your kite.
The drag depends on the drag coefficient, Cd, which depends on geometric properties of the kite and the angle between the kite surfaces and the wind. Drag coefficients are usually determined experimentally for aircraft, but the aerodynamic surfaces for most kites are simple, thin, flat plates. So we can use some experimental values of the drag coefficients for flat plates to get a first order idea of our kite performance. For a thin flat plate at a low angle of attack , the drag coefficient Cdo is equal to 1.28 times times the sine of the angle a:
Cdo = 1.28 * sin(a)
We use Cdo for the drag coefficient because there is another aerodynamic effect present on most kites. If we think of a kite as an aircraft wing, and use the terminology associated with aircraft wings, most kites have a low wing span (length from side to side) relative to the surface area. Most kites therefore have a low aspect ratio which is defined to be span squared divided by the area. Near the tips of a wing the flow spills from the underside to the topside because of the difference in pressure. This creates a downwash which changes the effective angle of attack of the flow over a portion of the wing. For low aspect ratio wings, the portion of the wing affected by the downwash is greater than for high aspect ratio wings. Since most kites have a low aspect ratio AR, we have to include the effect of the downwash on the drag coefficient. This effect is called the "drag due to lift" or the induced drag of the wing. The equation for induced drag is given at the bottom right of the slide:
Cd = Cdo + Cl^2 / (.7 * pi * AR) )
where Cl is the lift coefficient, the .7 is an efficiency factor for rectangular wing shapes, and pi is 3.14159.
With these equations you can make a first prediction of the drag of your kite. You can use the KiteModeler program to further study how kites work and to design your own kites.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov