
An excellent way for students to gain a feel for aerodynamic forces is to fly a kite. Students can also use math techniques learned in high school to determine the altitude of the kite during the flight.
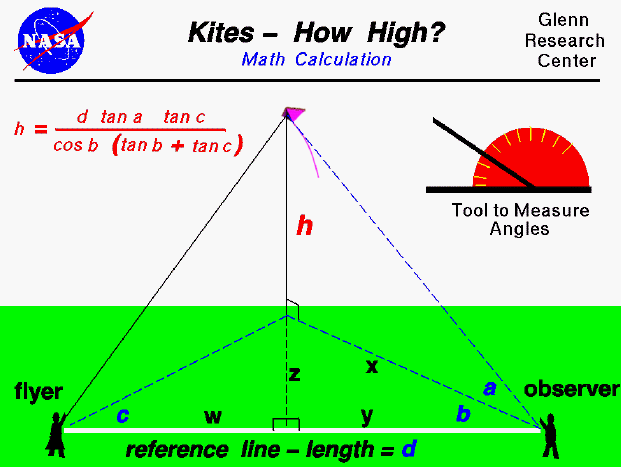
On this page we show a simple way to determine the altitude of a flying kite. The procedure requires an observer in addition to the kite flyer, and a tool (like the one shown in the upper portion of the figure) to measure angles. The observer is stationed some distance (d) from the flyer along a reference line. (You can lay a string of known length along the ground between the flyer and the observer to make this reference line. A long line will produce more accurate results.) To determine the altitude, the flyer calls out "Take Data", and measures the angle (c) between the reference line and the location of the kite. Notice that this measurement is taken parallel to the ground and can be done by the flyer measuring from the kite string to the reference line laid on the ground. When the observer hears the call, "Take Data", the observer must face the kite and measure the angle (a) from the ground to the kite. The observer must then measure the angle (b), parallel to the ground, between the direction the observer is facing and the reference line in the same manner as the flyer. (Notice that angle (a) is measured in a plane that is perpendicular to the ground while angles (b) and (c) are measured in plane parallel to the ground).
With the three measured angles and the measured distance between the flyer and the observer, we can use trigonometry to give us an equation for the altitude (h) of the kite. The equation is:
h = (d * tan a * tan c) / ( cos b * (tan b + tan c))
where the tangent (tan) and the cosine (cos) are trigonometric functions whose values are determined using a calculator.
If you are really good in math, see if you can derive this equation using the information given above. You can check your answer against my derivation. You can use this same equation to determine the height of any object from a tall tree to a flying model rocket. If you do not know trigonometry, you can still determine the altitude of the kite by using a graphical solution.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov