
A text only version of this slide is available which gives all of the flow equations. The interactive Java applet EngineSim is also available. This program solves these equations and displays the thrust and fuel flow values for a variety of turbine engines.
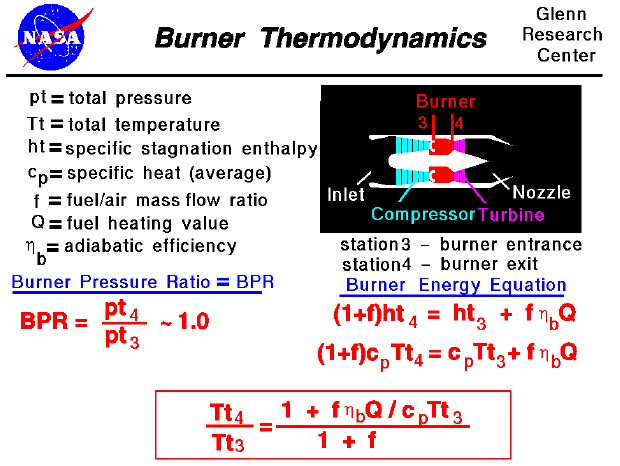
Most modern passenger and military aircraft are powered by gas turbine engines, which are also called jet engines. There are several different types of jet engines, but all jet engines have some parts in common. All jet engines have a combustor or burner in which the air and fuel are mixed and burned. The burning occurs at a higher pressure than free stream because of the action of the compressor. The pressure in the burner remains nearly constant during burning, decreasing by only 1 to 2 per cent. Using our station numbering, the burner pressure ratio (BPR) is equal to pt4 divided by pt3 and is nearly equal to one as shown on the slide.
As opposed to the compressor and power turbine, we cannot simply relate the total temperature ratio in the burner to the total pressure ratio because the physical processes are different. In the compressor and turbine, no heat enters the domain. Under those conditions the pressure ratio and temperature ratio are related. In the burner, heat is released in the combustion process, and the energy equation must be used to determine the temperature change. The energy equation is given on the right side of the slide, beneath the schematic picture. Since we are adding fuel in the domain, we account for the added mass of the fuel by using the fuel to air mass flow ratio (f). The specific enthalpy (enthalpy per mass) exiting the domain is equal to the specific enthalpy entering the domain plus the heat released during combustion. The heat release (Q) depends on the particular fuel that is being burned and is determined experimentally. An efficiency factor is applied, as well, to account for losses during burning. The enthalpy is equal to the specific heat coefficient at constant pressure (cp) times the temperature which leads to the second energy equation on the slide. With a little algebra, this energy equation can be solved for the temperature ratio across the burner. The temperature ratio is given in the red box at the bottom of the slide.
The burner entrance temperature (Tt3) is determined by the compressor and the external flow conditions. The fuel heating value (Q) is a property of the particular fuel being used, and the specific heat coefficient (cp) is a known property of air. In engine operation, we can set the fuel flow rate which determines a value for the fuel/air ratio (f) and sets the temperature ratio in the burner. The burner temperature ratio and pressure ratio determine a value for the engine temperature ratio (ETR), and engine pressure ratio (EPR) which in turn determine the theoretical engine thrust.
It would appear that we can make the temperature ratio (and resulting thrust) as large as we want by just increasing the fuel flow rate (and the fuel/air ratio). However, the details of the combustion process sets some limits on values of the fuel/air ratio. And in engine operation, there is a maximum burner exit temperature (Tt4) which is determined by material limits (http://www.ueet.nasa.gov/parts.htm). If we try to run the engine hotter than this maximum temperature, the burner and the turbine will be damaged. You can now use EngineSim to study the effects of different materials on engine operation.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov