
A text only version of this slide is available which gives all of the flow equations. The interactive Java applet EngineSim is also available. This program solves these equations and displays the thrust and fuel flow values for a variety of turbine engines.
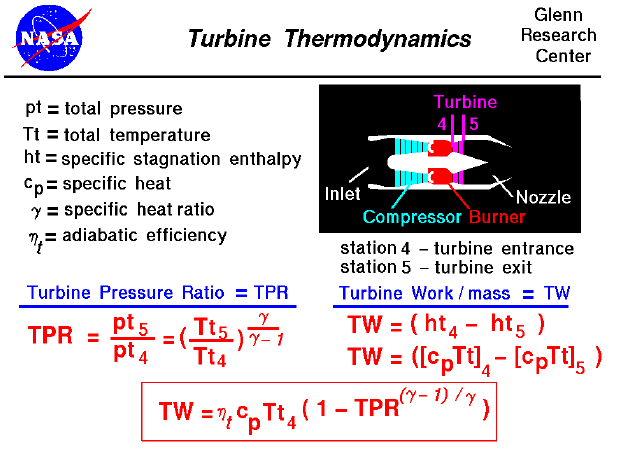
Most modern passenger and military aircraft are powered by gas turbine engines, which are also called jet engines. There are several different types of jet engines. But all jet engines have some parts in common. All jet engines have a turbine to drive the compressor. The job of the turbine is to extract energy from the heated flow exiting the burner. The turbine is connected to the shaft, which is also connected to the compressor. As the flow passes through the turbine, the total pressure (pt) and temperature (Tt) decrease. We measure the decrease in pressure by the turbine pressure ration (TPR), which is the ratio of the air pressure exiting the turbine to the air pressure entering the turbine. This number is always less than 1.0. Referring to our station numbering, the turbine entrance is station "4" and the turbine exit (nozzle entrance) is station "5". The TPR is equal to pt5 divided by pt4, as shown above.
In the axial turbine, cascades of small airfoils are mounted on a shaft that turns at a high rate of speed. Since no external heat is being added to or extracted from the turbine during this process, the process is isentropic. The temperature ratio across the turbine is related to the pressure ratio by the isentropic flow equations.
Work is done by the flow to turn the turbine and the shaft. From the conservation of energy, the turbine work per mass of airflow (TW) is equal to the change in the specific enthalpy of the flow from the entrance to the exit of the turbine. (The term "specific" means per mass of airflow.) The enthalpy at the entrance and exit is related to the total temperature at those stations, as shown at the right on the slide. Using algebra, we arrive at the equation in the box at the bottom of the slide that relates the work done by the turbine to the turbine pressure ratio, the incoming total temperature, some properties of the gas (specific heats [cp] and heat ratios [gamma]), and an efficiency factor (nt). The efficiency factor is included to account for the actual performance of the turbine as opposed to the ideal, isentropic performance. In an ideal world, the value of the efficiency would be 1.0. In reality, it is always less than 1.0. Because of mechanical inefficiencies, you cannot get 100% of the available work from the turbine.
The turbine blades exist in a much more hostile environment than compressor blades. Sitting just downstream of the burner, the blades experience flow temperatures of more than a thousand degrees Fahrenheit. Turbine blades must, therefore, be made of special materials (http://www.ueet.nasa.gov/parts.htm). that can withstand the heat, or they must be actively cooled. You can now use EngineSim to study the effects of different materials on engine operation.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov