During the fall of 1901, the brothers began to question the aerodynamic
data on which they were basing their aircraft designs.
They decided to
conduct a series of
wind tunnel tests
to verify the results they were
experiencing
in flight.
They would measure the aerodynamic lift and drag
on small
models
of their wing designs using a
wind tunnel
in their bicycle shop in Dayton, Ohio.
They built two separate balances to perform these measurements,
one for
lift.
and the other for
drag.
On this page we will discuss
the operation of the lift balance.
Because of the form of the
lift equation
used by the brothers, they were interested in measuring
the lift generated by a model relative to the drag of a reference flat plate.
The operation of the balance depends on the concepts of
torques
and
equilibrium.
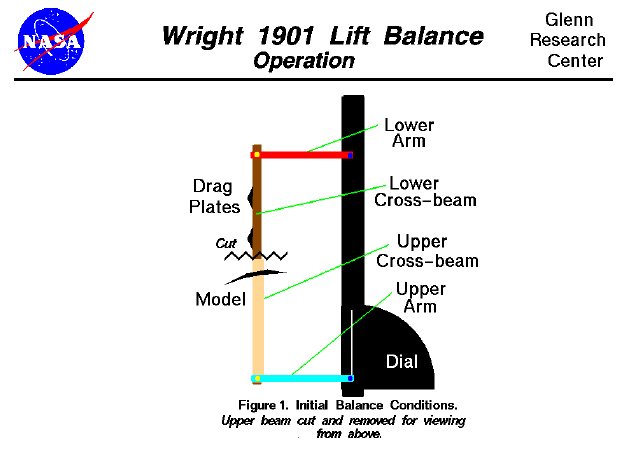
As the test begins, the tunnel is turned off and the
upper and lower cross beams are moved so that the upper beam lies on
top of the lower beam and the arms are parallel with the sides of the
tunnel as shown in the figure at the top of this page.
In this drawing, we are using the same color scheme as used on the page
describing the
design
of the lift balance.
We are looking down onto the balance from above and we have
cut the upper beam (saw-toothed line) so that we can see the orientation of the
lower beam and arm.
The lower beam holds the reference drag plates, while the upper beam
holds the model being tested.
The fan which pushes air through the tunnel is far to the right of this drawing.
The model is set to some desired
angle of attack
and the fan is turned on.
The cross beams and arms move because of torques
generated by the drag force of the plates and the lift and drag force of the
model on the long axles.
Because the friction sleeve is engaged, the upper and lower beams move together.
When the torque created by the drag plates and the drag of the model is
balanced by the torque generated by the lift of the model, the
balance no longer moves and assumes the following orientation:
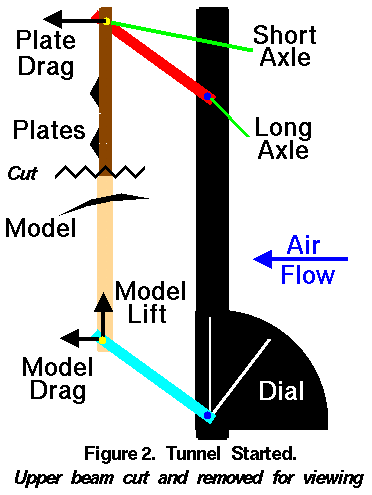
We have again cut the upper beam so that you can see the lower beam
and arm.
On this figure we show the direction of the forces by the small arrows.
We have placed the forces at the short axles because that is where the forces
generated by the model and plates are transmitted to the arms.
(Since the cross-beams are supported at both ends, and there are two arms at
each end, each arm actually transmits one fourth of the force.)
The arms transmit the force to the long axle and eventually to the frame and
tunnel walls. As the arms rotate because of the torque, the pointer of the dial
rotates as well. The pointer is always perpendicular to the lower arm.
To eliminate the torque produced by the drag of the model, the friction sleeve
is dis-engaged and the upper cross
beam is moved until the arm is parallel to the side of the tunnel.
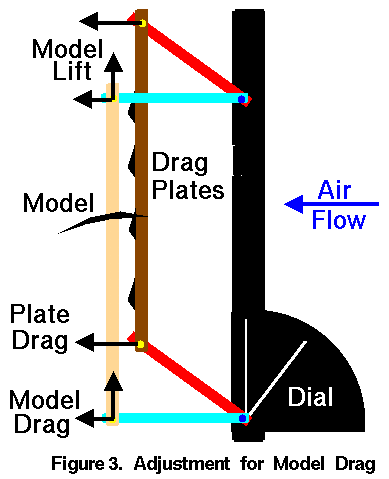
The bottom cross beam does not move because the the friction sleeve
is dis-engaged during the adjustment
and the dial pointer continues to record the amount
of rotation of the long axle.
When the sleeve is re-engaged,
the balance achieves a new equilibrium because of the torques of the plates
and the torque of the model on the long axles.
Several adjustments must be made until the upper arms remain parallel to the
side of the tunnel.
The torque about a point on an object is equal to the force applied to the object times
the perpendicular distance from the point to the place where the force is
applied.
This figure shows the magnitude and orientation of the torques on the long axles.
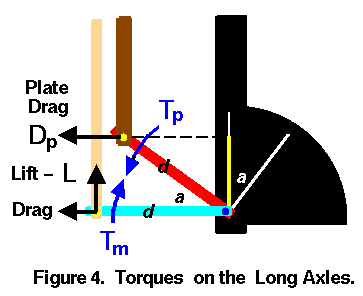
Because the drag of the model is alligned with the long axle,
the distance from the long axle measured perpendicular to the
model drag force is zero, and the model drag does not exert any torque
on the long axle.
The distance from the long axle perpendicular to the lift force
is the arm length (d).
The direction of the lift force (L) generates a torque from the model (Tm)
in the clockwise direction.
Tm = L * d
The distance from the long axle perpendicular to the plate drag force
is shown on Figure 4. by a yellow line near the dial.
The length of this line is the arm length (d) times the
sine
of the
angle (a) at which the lower arm is inclined.
The direction of the plate drag force (Dp) generates a
torque from the plate (Tp)
in the counter-clockwise direction.
Tp = Dp * d * sin(a)
In equilibrium, these torques are equal and the long axle does not rotate.
Tm = Tp
L * d = Dp * d * sin(a)
sin(a) = L / Dp
We can get a mathematical relation for the lift of the model from the
lift equation.
L= k * V^2 * Am * cl
where (k) is the
Smeaton coefficient,
(V) is the velocity, (Am) is the surface area of the model,
and (cl) is the lift coefficient.
Similarly, for the reference plates the
drag equation is:
D= k * V^2 * Ap * cd
where (Ap) is the area of the drag plates, and
(cd) is the drag coefficient.
Substituting into the torque equilibrium equation:
sin(a) = (k * V^2 * Am * cl) / (k * V^2 * Ap * cd)
For a flat plate, the drag coefficient is equal to 1.0. Cancelling
out similar variables we get
cl = sin(a) * Ap / Am
Notice that the angle (a) between the upper and lower arms is also
the angle recorded on the lift dial from the vertical reference line to
the pointer attached to the long axle. Knowing the area of the drag plates
and area of the model, the Wrights determined the lift coefficient by
recording the angle on the dial and solving the equation given above.
They repeated the test process many times, changing models and angle of attack
of the models to generate graphs of their results.
You can do the same thing, on-line, with an interactive
computer simulation
of the the tunnel and balance which we have developed.
Observations
There are several interesting aspects to the operation of the balance. At
the time the brothers began testing, they doubted both the value of Smeaton's
pressure coefficient (k) and the data curves produced by Otto Lilienthal that used
the Smeaton coefficient to determine cl. The two problems seemed to be locked together.
But notice that the
equation for determining the lift coefficient from the measured angle contains
no reference to Smeaton's coefficient. By balancing the model lift against the
flat plate drag, the brothers were able to separate the two problems. They were
then able to determine their own value for the Smeaton coefficient based on
their kite and glider experiments, and their own (correct) values for the lift coefficient
from the 1901 wind tunnel.
It is also interesting to note the role that the area ratio plays in the
lift coefficient equation. The maximum value for the sin(a) is 1.0 (at a = 90 degrees).
Without the area ratio, one could never get a lift coefficient greater
than 1.0. Or to put it another way, with the area of the plates equal to the
area of the model, if the lift of the model is greater than the drag of the
plates (cl > 1.0), the upper beam can not be adjusted to remove the drag of
model; it won't balance with the upper arm parallel to the side of the tunnel.
On the brothers' balance, the total area of the drag plates was 8 square inches.
The area of the models ranged from 3 to 8 square inches, with most of them
at 6 square inches. Several of the 6 square inch models had lift coefficients
greater than 1.0, which initially surprised Wilbur Wright.
Navigation..



- Beginner's Guide Home Page
|
