In 1899, when Wilbur Wright decided to "add my mite to help on
the future worker who will attain final success" in flight, he wrote
to the Smithsonian to obtain technical pamphlets on the state of the
art in aerodynamics. He and Orville learned that there were
mathematical equations which could
be used to predict the amount of
lift
and
drag
that an object would generate.
The equations from 1900 are slightly different than the equations for
lift
and
drag
that we use today, because of the reference conditions that are used
to define the lift and drag coefficients. Today we base our lift
and drag coefficients on the
dynamic pressure
of the moving air (or vehicle). Modern lift and drag coefficients are
factors which multiply the dynamic pressure times the
reference area of the object.
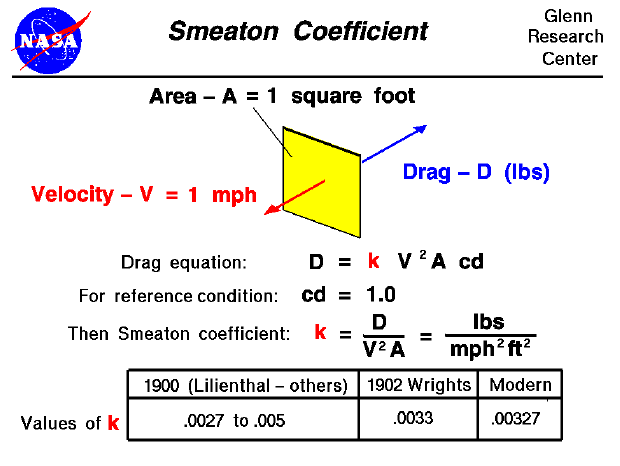
At the time of the Wright brothers, the reference conditions for the
lift and drag was the drag on a one square foot flat plate moving
at one mile per hour.
The lift and drag coefficients then become the ratio of the
lift and drag of the object to the drag of a flat plate of the same
area.
The flat plate reference was chosen as a standard because
people thought it would be an easy number to measure accurately.
In fact, because the flow past a flat plate can be quite unsteady, and
because it is hard to accurately measure a small velocity (1 mph), it is
a very difficult measurement to make. Published values of the "pressure
factor" had a range of values from .0027 to .005. The earliest published
value (.005) was from the Englishman, John Smeaton, and so the pressure factor
was named after him.
Besides being hard to accurately measure, the factor presents some other
problems for its users. The units given here are "mixed English". The velocity
is in miles per hour, the area in square feet, and the force in pounds
(slugs * foot per second squared). This means that to use the quoted value
of the factor in the given aerodynamic equations, one has to measure
the velocity in miles per hour (and then square it)
and the area is square feet. A metric version of the coefficient is also
available, but the physical reference is different; a
one meter square moving at one meter per second generates a drag force of
.13 kilograms (force).
Comparing with the
modern dynamic pressure reference, the Smeaton coefficient is only good at
one altitude. From the modern theory, we know that the aerodynamic forces
depend on the density of the air, and the density varies with altitude.
Using the Smeaton reference, a different value for the
coefficient would be required at each altitude, because the drag of a flat
plate changes with altitude. Fortunately, the early Wright aircraft could
not climb high enough for the change in air density to make a difference.
When the Wrights began to design the 1900 aircraft,
they used values for the lift coefficient based on the work by Lilienthal.
Lilienthal and the Wrights used the .005 value for the pressure factor.
During the kite and glider
experiments of 1900 and 1901, the brothers measured the performance
of their aircraft. Neither aircraft performed as well as predicted
by the lift equation. The 1901 aircraft
had been designed to lift itself (100 pounds) plus a pilot (150 pounds)
when flown as a kite in a 15 mile per hour wind at 5 degrees angle of attack.
But in flight, it could barely lift itself in a 15 mile per hour wind at
a much higher angle of attack.
So the brothers began to doubt the .005 value for the Smeaton coefficient.
They determined that a value of .0033 more closely
approximated their flight data.
We can derive the true value of the Smeaton coefficient by using the modern
drag equation:
D = .5 * Cd * r * V^2 * A
The drag equation states that drag (D) is equal to the
drag coefficient (Cd) times the density of the air (r) times half of the
square of the velocity (V) times the wing area (A).
From the definition of the Smeaton coefficient:
k = D / (U^2 * A)
Where we have used (U) for the velocity because this velocity is measured
in miles per hour, while the (V) of the modern drag equation
is measured in feet per second. Substituting:
k = Cd * .5 * r * (V^2/ U^2)
The measured
drag coefficient
for a low speed flat plate is 1.28, the air density (r) is .00237 slug/ft^3
and 88 feet per second equals 60 miles per hour. Substituting:
k = 1.28 * .5 * .00237 * 88 * 88 / 60 / 60
k = .00327
The Wright brothers were very close to this value using their
experimental data.
Navigation..



- Beginner's Guide Home Page
|
