Between 1900 and 1905, the Wright brothers designed and built three
unpowered gliders and three powered aircraft.
As they designed each aircraft, how
did they know how big to make the wings?
The Wright brothers operated a bicycle shop in
Dayton, Ohio, and had a good working knowledge of math and science.
They knew about
Newton's laws
of motion and about
forces
and
torques.
They knew that they needed to generate enough
aerodynamic lift
to overcome the
weight
of their aircraft.
They had written to the Smithsonian when they began their enterprise in 1899
and received technical papers describing the aeronautical
theories of the day. There were mathematical equations which could
be used to predict the amount of lift
and
drag
that an object would generate. The
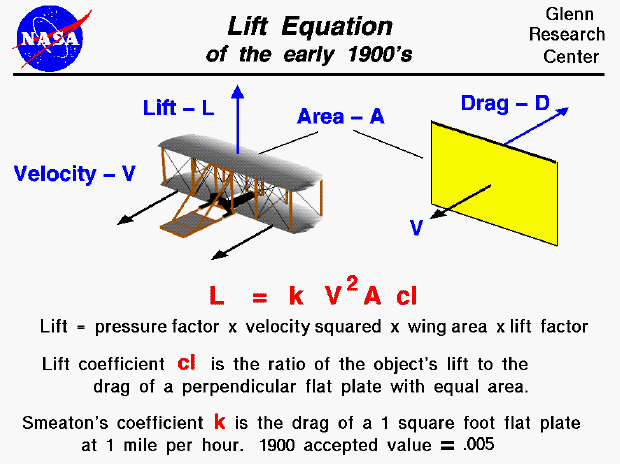
lift equation is shown on this slide.
The amount of lift generated by an object depends on a number of factors,
including
properties
of the air, the
velocity between the object and the
air, the surface area
over which the air flows, the
shape
of the body, and the body's inclination to the flow, also called the
angle of attack.
By the time the Wrights began their studies, it had been determined that
lift depends on the
square of the velocity
and varies linearly
with the surface area of the object.
Early aerodynamicists characterized the dependence on the properties of the air
by a pressure coefficient called
Smeaton's coefficient which represented the
pressure force (drag) on a one foot square flat plate moving at one mile per hour through
the air. They believed that any object moving through the air converted some
portion of the pressure force into lift, and they represented that portion by a
lift coefficient. The resulting equation is given as:
L = k * V^2 * A * cl
where L is the lift, k is the Smeaton coefficient, V is the velocity,
A is the wing area, and cl is the lift coefficient.
This equation is slightly different from the modern
lift equation
used today. The modern equation uses the
dynamic pressure
of the moving air for the pressure dependence, while this equation uses
the Smeaton coefficient. Modern lift coefficients relate the lift force on the object to
the force generated by the dynamic pressure times the area, while the 1900's
lift coefficients relate the lift force to the drag of a flat plate of equal area.
The 1900's equation assumes that you know the perpendicular pressure force on a
moving flat plate (Smeaton coefficient). Because
of measuring inaccuracies at the time, there were many quoted values for the
coefficient ranging from .0027 to .005. Lilienthal had used the .005 value
in the design and testing of his wings.
When the Wrights began to design the 1900 aircraft,
they used values for the lift coefficient based on the work by Lilienthal
so they too used the .005 value.
During the kite and glider
experiments of 1900 and 1901, the brothers measured the performance
of their aircraft. Neither aircraft performed as well as predicted
by the lift equation. The 1901 aircraft
had been designed to lift itself (100 pounds) plus a pilot (150 pounds)
when flown as a kite in a 15 mile per hour wind at 5 degrees angle of attack.
But in flight, it could barely lift itself in a 15 mile per hour wind at
a much higher angle of attack.
So the brothers began to doubt the .005 value for the Smeaton coefficient and
they determined that a value of .0033 more closely approximated their data.
The modern accepted value is .00326.
The brothers also began to doubt the accuracy of Lilienthal's lift
coefficients.
So in the fall of 1901, they decided to determine their own values
for the lift coefficient using a
wind tunnel.
The brothers built a clever
balance
to directly measure the ratio of the lift of their models to the
drag of an equivalent flat plate.
We have developed an
interactive tunnel simulator
so that you can duplicate their wind tunnel results.
In the
process
of testing many airfoil models, the brothers discovered the importance
of wing
shape
on the lift coefficient.
They determined that the Lilienthal data was correct for the wing geometry
that he had used, but that the data could not be applied to a wing with a very
different geometry. Lilienthal's wings had a rather short span and an elliptical
planform, while the brothers used a long, thin, rectangular planform.
The brothers tested over fifty different models to determine
how lift and drag are affected by various design parameters
and they used this data to design their 1902 aircraft
using the lift equation shown on the slide with their own lift coefficients.
You can view a short
movie
of "Orville and Wilbur Wright" discussing the lift force
and how it affected the flight of their aircraft. The movie file can
be saved to your computer and viewed as a Podcast on your podcast player.
Navigation..



- Beginner's Guide Home Page
|
