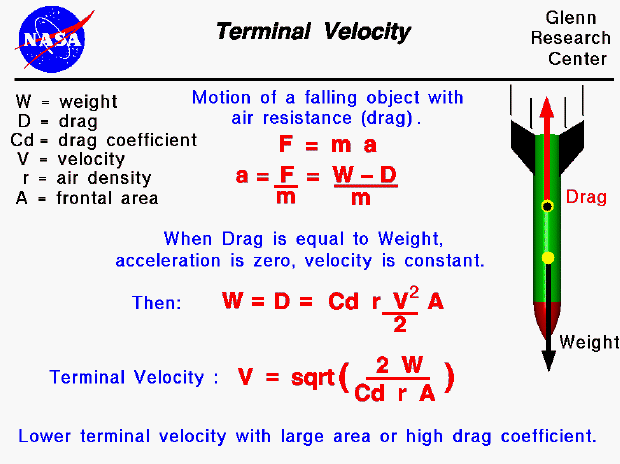

An object which is falling through the atmosphere is subjected to two external forces. One force is the gravitational force, expressed as the weight of the object. The other force is the air resistance, or drag of the object. The motion of a falling object can be described by Newton's second law of motion (Force equals mass times acceleration -- F = m a) which can be solved for the acceleration of the object in terms of the net external force and the mass of the object (a = F / m). The net external force (F) is equal to the difference between the weight and the drag forces (W - D). When drag is equal to weight, there is no net external force on the object and the object will fall at a constant velocity as described by Newton's first law of motion. The constant velocity is called the terminal velocity .
We can determine the value of the terminal velocity by doing a little algebra and using the drag equation. Drag (D) depends on a drag coefficient, (Cd) the air density, (r) the square of the air velocity (V) and some reference area (A) of the object.
D = Cd * r * V ^2 * A / 2
At terminal velocity, D = W. Solving for the velocity, we obtain the equation
V = sqrt ( (2 * W) / (Cd * r * A)
Typical values of the drag coefficient are given on a separate slide. For a model rocket, the value is near 0.75. Because model rockets do not fly very high, the air density is nearly constant and equal to the sea level value (.00237 slug/cu ft or 1.229 kg/cu m).
The terminal velocity equation tells us that an object with a large cross-sectional area or a high drag coefficient will fall slower than an object with a small area or low drag coefficient. A rocket with a large parachute will fall slower than one with a streamer recovery system. Since a rocket will drift with the wind, you can make your rocket return closer to the pad on a windy day by using a streamer.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov