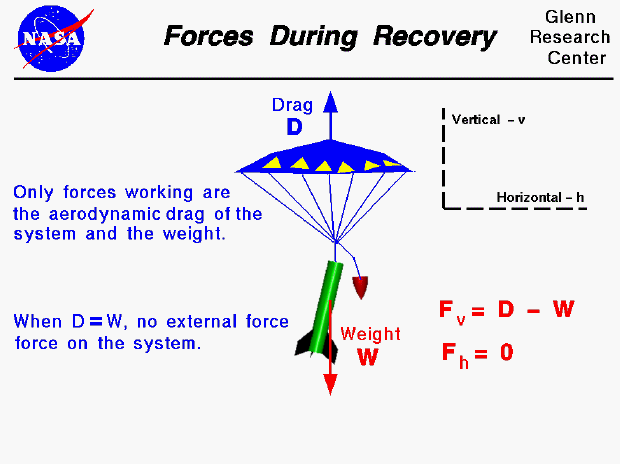

The forces on a model rocket change dramatically in both magnitude and direction throughout a typical flight. This figure shows the forces on a rocket during the recovery portion of the flight. At the end of the powered portion of the flight, the model rocket uses up all its fuel, the engine goes out and the thrust goes to zero. The rocket then coasts upward until the velocity goes to zero and the maximum altitude is reached. Because weight is still acting on the rocket, it immediately begins to fall back to earth. To slow the descent, an explosive charge is used to deploy a parachute. As the rocket falls, only two forces are acting on the rocket, the weight of the rocket and the aerodynamic drag on the parachute.
The weight (W) is always directed towards the center of the earth. By definition, the aerodynamic drag (D) is opposed to the flight direction. As the rocket descends, the drag and the weight are opposing forces. If we neglect the effects of the wind on the descending rocket, the horizontal force (Fh) is zero.
Fh = 0
The vertical force (Fv) is the drag minus the weight.
Fv = D - W
The acceleration of the rocket can be determined by solving Newton's second law of motion. The drag depends on the square of the velocity,. The rocket is falling at a high rate of speed when the parachute is deployed so the drag is high. The point is quickly reached where the drag is equal and opposite to the weight and the acceleration then becomes zero. The rocket then falls at a constant terminal velocity as predicted by Netwon's first law of motion. We can determine the magnitude of the terminal velocity by equating the drag and the weight and solving for the velocity, as shown on a separate slide.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov