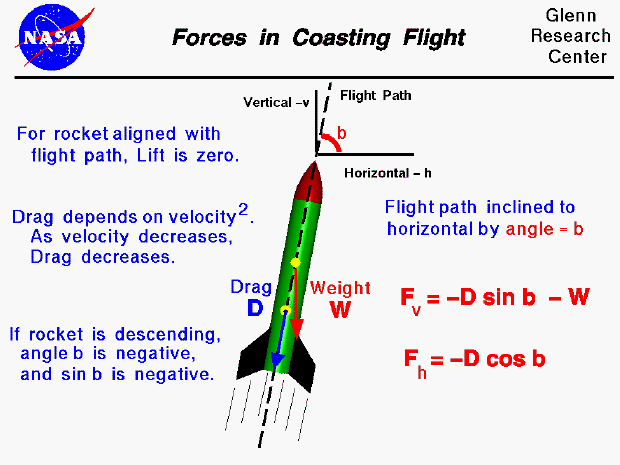

The forces on a model rocket change dramatically in both magnitude and direction throughout a typical flight. This figure shows the forces on a rocket during the coasting portion of the flight. At the end of the powered ascent, the model rocket uses up all its fuel, the engine goes out and the thrust goes to zero. The only remaining forces acting on the rocket are the weight, and the aerodynamics (lift and drag).
Considering the forces on the model rocket, the weight (W) is always directed toward the center of the earth. If the axis of the rocket is perfectly aligned with the flight path, the lift will be zero due to the symmetry of the rocket. If the axis of the rocket is not aligned with the flight path, lift is generated which stabilizes the rocket and brings it back into alignment. By definition, the drag (D) is directed along the flight path. The amount of drag depends on several factors including the shape and size of the rocket and the square of the rocket velocity which changes throughout the coasting portion of the flight. During the upward coast, the weight and drag both oppose the motion of the rocket. The rocket is constantly slowing down and the magnitude of the drag force is constantly decreasing. Eventually, a point is reached where the vertical velocity is zero and the rocket can go no higher. You can determine this maximum height by some rather simple angle and distance measurements and using trigonometry. Because the weight is still acting on the rocket, the rocket will then begin to fall back to earth. Initially, the velocity is low and the drag, which is now in a direction opposite to the weight, is much smaller than the weight. The rocket gains speed as it falls. Since the speed increases, the drag increases and a point is soon reached where the drag is equal and opposite to the weight. Under these conditions, there is no net force acting on the rocket, and from Newton's first law, the rocket falls at a constant terminal velocity.
During coasting flight, the flight path will normally be inclined to the local vertical and horizontal because of the wind. We can then use trigonometry (which you learn in high school), to break the forces into a horizontal component and a vertical component using the inclination angle (b). The horizontal force (Fh) on the rocket is equal to
Fh = - D * cos b
where cos is the cosine of the angle. The vertical force (Fv) is given by
Fv = - D * sin b - W
where sin is the sine of the angle. The acceleration, velocity, and location of the rocket during coasting flight can be determined at any time during the flight by applying Newton's Second Law of Motion, making some simplifying assumptions, and using some math. During the descending coast, the inclination angle will be negative and the sine of the angle will also be negative. From the vertical acceleration equation we can see that the drag and weight are in then in opposition (the drag term is positive and the weight term is always negative).
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov