
Flying model rockets is a relatively safe and inexpensive way for students to learn the basics of aerodynamic forces and the response of vehicles to external forces. Students can also use math techniques learned in high school to determine the performance of the rocket during the. flight.
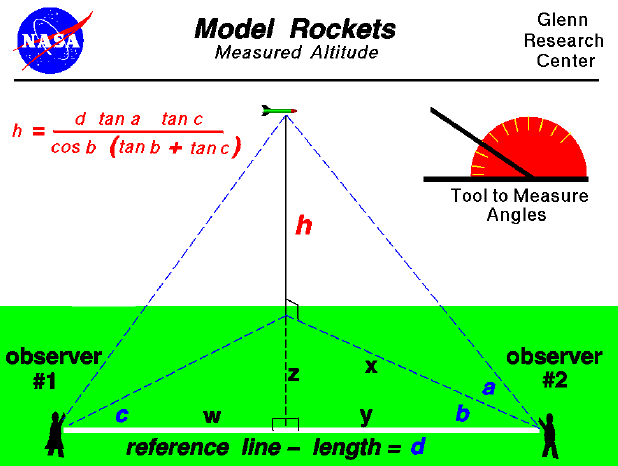
On this slide we show a simple way to determine the maximum altitude the rocket reaches at the end of the coasting flight. The procedure requires two observers and a tool like the one shown in the upper portion of the figure to measure angles. The observers are placed some distance (d) apart along a reference line which is shown in white on the figure. You can lay a string of known length along the ground between the observers. As the rocket passes its maximum altitude, observer #1 calls out "Take Data", and measures the angle (c) between the reference line and the location of the rocket. Notice that this measurement is taken parallel to the ground and can be done by the observer facing the rocket, holding position, and measuring from the direction the observer is facing to the reference line on the ground. When the second observer hears the call, "Take Data", the observer must face the rocket and measure the angle (a) from the ground to the rocket. The second observer must then measure the angle (b), parallel to the ground, between the direction the observer is facing and the reference line in the same manner as the first observer. (Notice that angle (a) is measured in a plane that is perpendicular to the ground while angles (b) and (c) are measured in plane parallel to the ground).
With the three measured angles and the measured distance between the observers, we can use trigonometry to give us an equation for the altitude (h) of the rocket. The equation is
h = (d * tan a * tan c) / ( cos b * (tan b + tan c))
where the tangent (tan) and the cosine (cos) are trigonometric functions whose values are determined using a calculator.
If you are really good in math, see if you can derive this equation using the information given above. You can check your answer against my derivation. You can use this same equation to determine the height of any object from a tall tree to a flying kite. If you do not know trigonometry, you can still determine the altitude of an object by using a graphical solution.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov