
The interactive Java applet EngineSim solves these equations and displays the thrust and fuel flow values for a variety of turbine engines.
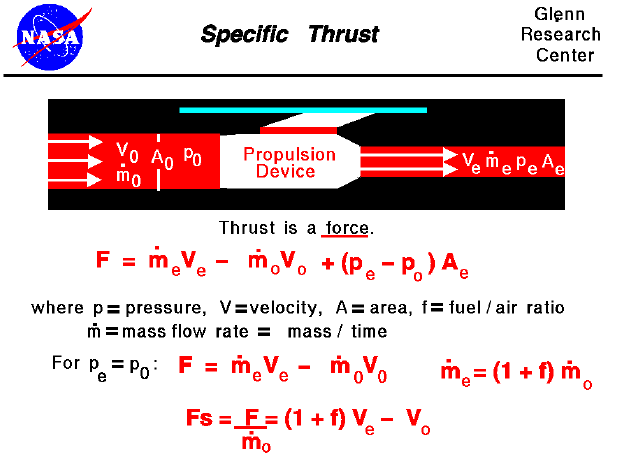
Thrust is the force which moves an aircraft through the air. Thrust is generated by the engines of the airplane through the reaction of accelerating a mass of gas. The gas is accelerated to the the rear and the engine (and aircraft) is accelerated in the opposite direction. To accelerate the gas, we need some kind of propulsion system. We will discuss the details of various propulsion systems on some other pages. For right now, let us just think of the propulsion system as some machine which accelerates a gas.
From Newton's second law of motion, we can define a force to be the change in momentum of an object with a change in time. Momentum is the object's mass times the velocity. When dealing with a gas, the basic thrust equation is given as:
F = mdot e * Ve - mdot 0 * V0 + (pe - p0) * Ae
Thrust (F) is equal to the exit mass flow rate (mdot e) times the exit velocity (Ve) minus the free stream mass flow rate (mdot 0) times the free stream velocity (V0) plus the pressure difference across the engine (pe - p0) times the engine area (Ae). For gas turbine engines, the nozzle is usually designed to make the exit pressure equal to free stream. In that case the thrust equation simplifies to:
F = mdot e * Ve - mdot 0 * V0
We further note that the exit mass flow rate is equal to the incoming mass flow rate plus the fuel flow rate. Using the fuel to air mass flow ratio (f), we obtain:
mdot e = (1 + f) * mdot 0
Now using a little algebra, we can define a new variable called the specific thrust (Fs) which depends only on the velocity difference produced by the engine:
Fs = F / mdot 0 = (1 + f) * Ve - V0
A "specific" property does not depend on the mass of that property. We can easily compute the exit velocity if we know the engine pressure ratio (EPR), the engine temperature ratio (ETR), and the nozzle performance. The EPR and ETR depend on the component pressure and temperature ratios which are given on each of the component thermodynamic slides. With this information, we can easily compute the thrust of an engine.
Why are we interested in specific thrust? First, it is an indication of engine efficiency. Two different engines will have different values of specific thrust. The engine with the higher value of specific thrust is more efficient because it produces more thrust for the same amount of airflow. Second, it simplifies our mathematical analysis of jet engine thermodynamics. The math concerning work and energy contains the mass flow rate as a multiplier. We could carry it along, but since the mass flow rate is a constant, the math is easier if we just divide it out at the beginning and put it back in at the end. Third, it gives us an easy way to "size" an engine during preliminary analysis. The result of our thermodynamic analysis is a certain value of specific thrust. The aircraft drag will define the required value of thrust. Dividing the thrust required by the specific thrust will tell us how much airflow our engine must produce and this determines the physical size of the engine.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov