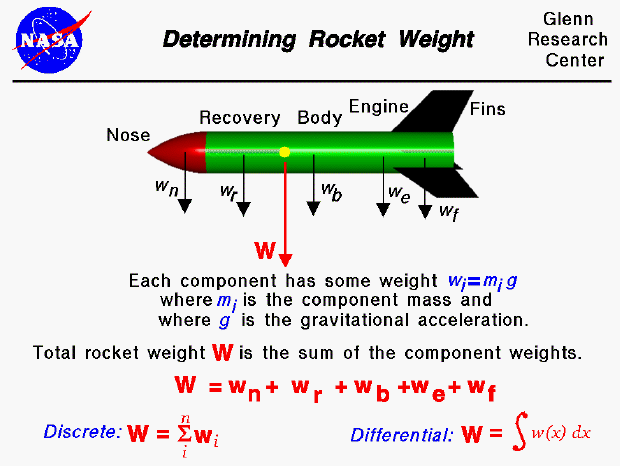
Weight is the force generated by the gravitational attraction of the earth on the model rocket. The mass (and weight) is actually distributed throughout the rocket and for some problems it is important to know the distribution. But for rocket trajectory and stability, we only need to be concerned with the total weight and the location of the center of gravity. The center of gravity is the average location of the mass of the rocket.
How do engineers determine the rocket weight?
In general, determining the weight is a complicated procedure requiring the use of calculus. We'll discuss the general answer at the bottom of this page. This figure shows a simplified version of this calculation which can be used by secondary students. For this figure, we assume that we already know the weight of each of the major parts of the rocket (the nose, recovery system, body tube, engine, and fins). The individual component weight is simply the mass of the component times the gravitational constant, g , which is 32.2 ft/square sec in English units and 9.8 meters/square sec in metric units. The total weight of the rocket is simply the sum of all the individual weights of the components.
We can generalize the addition of component weights and the result is the "discrete" version shown at the lower left of the figure. The zig-zag symbol is the greek letter sigma - which indicates summation. The "i" below the sigma is an index, and the index goes from 1 to some number "n", which is the total number of parts. So this equation says that the weight of the rocket is equal to the sum of the weight of "n" parts. This equation would work for "n" discrete parts, but what if the parts are not discrete? What if we had a continuous change of mass from front to back (as occurs for a balsa wood nose)? The continuous change can be computed using integral calculus, as shown in the "differential" equation at the lower right. The w(x) symbol represents the weight which is some function of distance x. If we are given the form of the function, there are methods to integrate the equation. If we don't know the actual functional form, we can still numerically integrate the equation using a spread sheet by dividing the distance up into a number of small distance segments and determining the average value of the mass (or weight) over that small segment.
Forces on a Model Rocket:
RocketModeler:
Rocket Modeler Talk:
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov