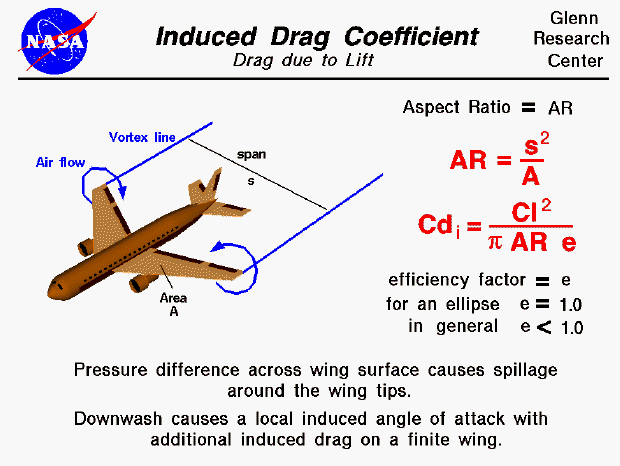

There are many factors which influence the amount of aerodynamic drag which a body generates. Drag depends on the shape, size, inclination, and flow conditions of the air passing the object. For a three dimensional wing, there is an additional component of drag, called induced drag, which will be discussed on this page.
For a lifting wing, the air pressure on the top of the wing is lower than the pressure below the wing. Near the tips of the wing, the air is free to move from the region of high pressure into the region of low pressure. The resulting flow is shown on the figure by the two circular blue lines with the arrowheads showing the flow direction. As the aircraft moves to the lower left, a pair of counter-rotating vortices are formed at the wing tips. The line of the center of the vortices are shown as blue Vortex lines leading from the wing tips. If the atmospheric conditions are right (high humidity), you can actually see the vortex lines on an airliner during landing. The vortices produce a down wash of air behind the wing which is very strong near the wing tips and decreases toward the wing root. The local angle of attack of the wing is increased by the induced flow of the down wash, giving an additional, downstream-facing, component to the aerodynamic force acting over the entire wing. This additional force is called induced drag because it faces downstream and has been "induced" by the action of the tip vortices. It is also called "drag due to lift" because it only occurs on finite, lifting wings and varies with the square of the lift.
The derivation of the equation for the induced drag is fairly tedious and relies on some theoretical ideas which are beyond the scope of the Beginner's Guide. The induced drag coefficient Cdi is equal to the square of the lift coefficient Cl divided by the quantity: pi (3.14159) times the aspect ratio AR times an efficiency factor e.
Cdi = (Cl^2) / (pi * AR * e)
The aspect ratio is the square of the span s divided by the wing area A. For a rectangular wing this reduces to the ratio of the span to the chord. Long, slender, high aspect ratio wings have lower induced drag than short, thick, low aspect ratio wings. (Induced drag is a three dimensional effect related to the wing tips. The longer the wing, the farther the tips are from the main portion of the wing, and the lower the induced drag.) Lifting line theory shows that the optimum (lowest) induced drag occurs for an elliptic distribution of lift from tip to tip. The efficiency factor e is equal to 1.0 for an elliptic distribution and is some value less than 1.0 for any other lift distribution. (The outstanding aerodynamic performance of the British Spitfire of World War II is partially attributable to its elliptic shaped wing which gave the aircraft a very low amount of induced drag.) A more typical value of e = .7 for a rectangular wing. The total drag coefficient, Cd is equal to the base drag coefficient at zero lift Cdo plus the induced drag coefficient Cdi.
Cd = Cdo + Cdi
The drag coefficient in this equation uses the wing area for the reference area. Otherwise, we could not add it to the square of the lift coefficient, which is also based on the wing area.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov