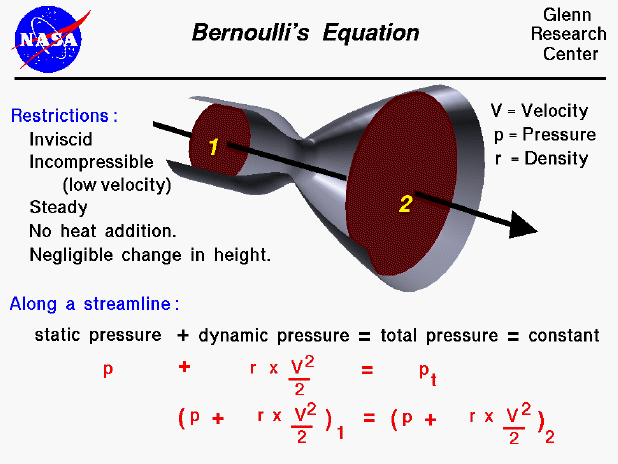

In the 1700s, Daniel Bernoulli investigated the forces present in a moving fluid. This slide shows one of many forms of Bernoulli's equation. The equation appears in many physics textbooks, as well as fluid mechanics and airplane textbooks. The equation states that the static pressure in the flow plus one half of the density times the velocity squared is equal to a constant throughout the flow, which we call the total pressure of the flow. Again, this is only one form of the equation and the restrictions for this form are that the flow is inviscid, incompressible, steady, without heat addition, and with negligible change in height. If we consider other properties of the fluid, we can derive other forms of the equation.
It is important when applying any equation that you are aware of the restrictions on its use; the restrictions usually arise in the derivation of the equation when certain simplifying assumptions about the nature of the problem are made. If you ignore the restrictions, you may often get an incorrect "answer" from the equation. For instance, this form of the equation was derived while assuming that the flow was incompressible, which means that the speed of the flow is much less than the speed of sound. If you use this form for a supersonic flow, the answer will be wrong.
The equation was originally derived by considering the conservation of mechanical energies within the fluid. The molecules within a fluid are in constant random motion and collide with each other and with the walls of an object in the fluid. The motion of the molecules gives the molecules a linear momentum; pressure is a measure of this momentum. If a gas is at rest, all of the motion of the molecules is random and the pressure that we detect is the total pressure of the gas. If the gas is set in motion or flows, some of the random components of velocity are changed in favor of the directed motion. We call the directed motion "ordered," as opposed to the disordered random motion.
We can associate a "pressure" with the momentum of the ordered motion of the gas. We call this pressure the dynamic pressure. The remaining random motion of the molecules still produces a pressure called the static pressure. At the molecular level, there is no distinction between random and ordered motion. Each molecule has a velocity in some direction until it collides with another molecule and the velocity is changed. But when you sum up all the velocities of all the molecules you will detect the ordered motion. From a conservation of energy and momentum, the static pressure plus the dynamic pressure is equal to the original total pressure in a flow (assuming we do not add or subtract energy in the flow). The form of the dynamic pressure is the density times the square of the velocity divided by two.
In the derivation of the equation, the dissipation of energy by viscous forces was neglected (inviscid flow), and there was no introduction of energy allowed (no heat addition). In the integration of the general equations, an assumption was also introduced that restricts this equation to be true only along a single streamline. If you have a flow with many streamlines, the total pressure is a constant along any streamline, but may vary from streamline to streamline. (If we make an additional assumption that the flow is irrotational, then the constant does not vary from streamline to streamline as long as the height difference is small. If the height distance between streamlines becomes large, you have to add a buoyancy term {density x gravity x height} to the left side. Irrotational flows are flows that conserve angular momentum, which seems fairly restrictive, but, in fact, occurs quite often in aerodynamics. An ideal source, sink, uniform flow, and point vortex are all irrotational flows.
The fluids problem shown on this slide is low speed flow through a tube with changing cross-sectional area. For a streamline along the center of the tube, the velocity will slow from station one to two. Bernoulli's equation would describe the relation between velocity, density, and pressure for this flow problem. Along a low speed airfoil, the flow is incompressible and the density remains a constant. Bernoulli's equation then reduces to a simple relation between velocity and static pressure. Since the velocity can vary along the streamline, this equation can be used to compute the change in pressure. The static pressure integrated along the entire surface of the airfoil will give the total aerodynamic force on a body. This force can be broken down into the lift and drag of the airfoil.
The equation is also used on aircraft to provide a speedometer called a pitot tube. A pressure is quite easy to measure with a mechanical device. In a pitot tube, we measure the static and total pressure and can then use Bernoulli's equation to compute the velocity.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov