Aerodynamicists use
wind tunnels
to test models of proposed aircraft.
In the tunnel, the engineer can carefully control the
flow conditions which affect
forces
on the aircraft. By making careful measurements of the forces on
the model, the engineer can predict the forces on the full scale
aircraft. And by using special diagnostic techniques, the engineer
can better understand and improve the performance of the aircraft.
Wind tunnels are designed for a specific purpose and
speed range and
there is a wide variety of
wind tunnel types
and model instrumentation.
The model to be tested in the wind tunnel is placed in the
test section
of the tunnel. The speed in the test section is determined by the design
of the tunnel.
The choice of speed range affects the
design of the wind tunnel
due to
compressibility effects.
On this slide we derive the equations which explain and describe why
a supersonic flow accelerates in the diffuser section of the tunnnel
while a subsonic flow decelerates in a divergent duct. We begin with the
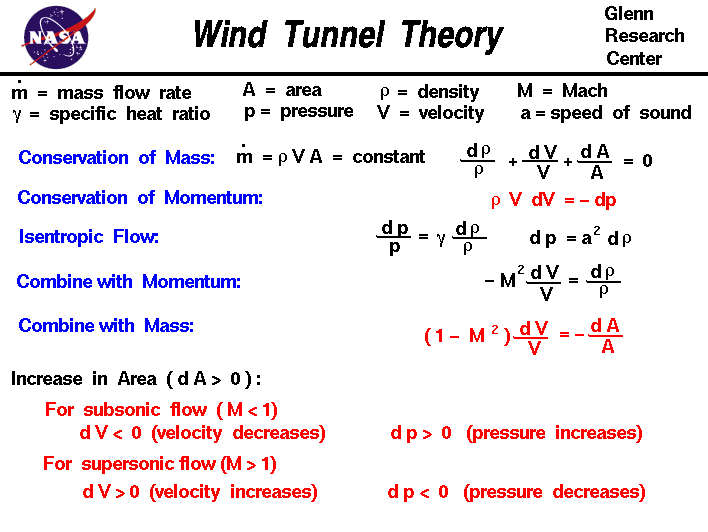
conservation of mass equation:
mdot = rho * V * A = constant
where mdot is the mass flow rate, rho is the gas
density, V is the gas velocity,
and A is the cross-sectional flow area. If we differentiate
this equation, we obtain:
V * A * drho + rho * A * dV + rho * V * dA = 0
divide by (rho * V * A) to get:
drho / rho + dV / V + dA / A = 0
Now we use the
conservation of momentum equation:
rho * V * dV = - dp
and an
isentropic flow relation:
dp / p = gam * drho / rho
where gam is the
ratio of specific heats.
This is Equation #10 on the page which contains the
derivation
of the isentropic flow relations
We can use algebra on this equation to obtain:
dp = gam * p / rho * drho
and use the
equation of state
p / rho = R * T
where R is the gas constant and T is temperature, to get:
dp = gam * R * T * drho
gam * R * T is the square of the
speed of sound a:
dp = (a^2) * drho
Combining this equation for the change in pressure with the momentum equation
we obtain:
rho * V * dV = - (a^2) * drho
V / (a^2) * dV = - drho / rho
- (M^2) * dV / V = drho / rho
using the definition of the
Mach number M = V / a.
Now we substitute this value of (drho /rho) into the mass flow equation to get:
- (M^2) * dV / V + dV / V + dA / A = 0
(1 - M^2) * dV / V = - dA / A
This equation tells us how the velocity V changes when the area A
changes, and the results depend on the Mach number M of the flow.
If the flow is subsonic then (M < 1) and the term multiplying the
velocity change is positive ([1 - M^2] > 0). Then an increase in the area
(dA > 0 ) produces a negative increase (decrease) in the velocity (dV < 0).
For a subsonic wind tunnel, the flow downstream
of the test section will decelerate and stay subsonic. For a
supersonic flow (M > 1) the term multiplying velocity change is negative
([1 - M^2] < 0). Then an increase in the area (dA > 0) produces an increase
in the velocity (dV > 0). This is exactly the opposite of what happens
subsonically.
Why the big difference? Because in supersonic (compressible)
flows, both the density and the velocity are changing as we change the area
in order to conserve mass. For subsonic (incompressible) flows,
the density remains fairly constant, so the increase in area produces a
decrease in velocity to conserve mass. But in supersonic flows, there are
two changes; the velocity and the density. The equation:
- (M^2) * dV / V = drho / rho
tells us that for M > 1, the change in density is much greater than
the change in velocity. To conserve both mass and momentum in a supersonic
flow, the velocity increases and the density decreases as the area is
increased.
Navigation ..



- Beginner's Guide Home Page
|
