Thermodynamics
is a branch of physics which deals with the energy
and work of a system. It was born in the 19th century as scientists
were first discovering how to build and operate steam engines.
Thermodynamics deals only with the
large scale response
of a system
which we can observe and measure in experiments.
As aerodynamicists, we are most interested in the thermodynamics of
propulsion systems
and
high speed flows.
On this page we consider the thermodynamics of a
four-stroke
internal combustion
engine.
Today, most general aviation or private airplanes are
powered by internal combustion (IC) engines, much like
the engine in your family automobile.
There are two main parts to engine operation: the
mechanical operation
of the
engine parts,
and the
thermodynamics
through which the engine produces
work
and
power.
On this page we discuss the basic thermodynamic equations that allow you
to design and predict engine performance.
In an internal combustion engine, fuel and air are
ignited
inside a cylinder. The hot exhaust pushes a piston which is connected
to a
crankshaft
to produce power. The burning of fuel is not a continuous process, but occurs
very quickly at regular time intervals. Between ignitions, the engine parts
move in a repeated sequence called a cycle.
The engine is called a four stroke engine because there are four movements, or
strokes,
of the piston during one cycle.
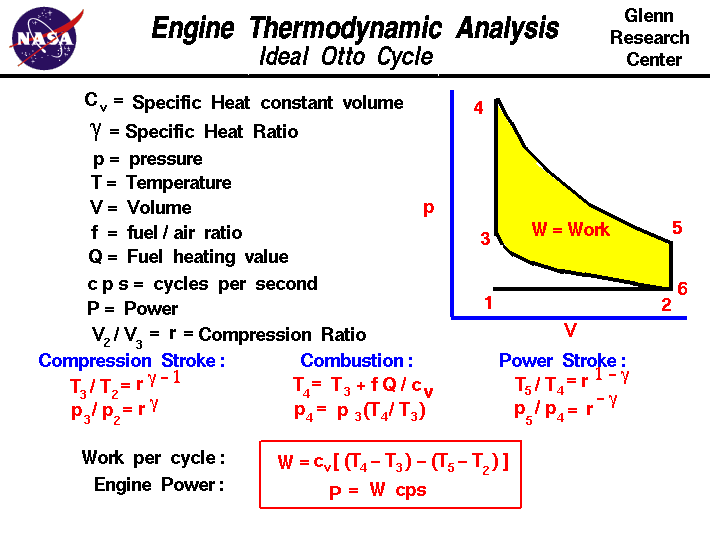
On the figure we show a
plot of
pressure
versus gas
volume
throughout one cycle.
We have broken the cycle
into six
numbered stages
based on the mechanical operation
of the engine.
For the ideal four stroke engine, the
intake stroke (1-2)
and
exhaust stroke (6-1)
are done at constant pressure and do not contribute to the generation
of power by the engine.
During the
compression stroke (2-3),
work is done on the gas by the piston. If we assume that no heat enters
the gas during the compression, we know the
relations
between the change in volume and the change in pressure and temperature
from our solutions of the
entropy equation
for a gas.
We call the ratio of the volume at the beginning of
compression to the volume at the end of compression the compression ratio,
r. Then
p3 / p2 = r ^ gamma
T3 / T2 = r ^ (gamma - 1)
where p is the pressure, T is the temperature, and gamma
is the ratio of
specific heats. During the
combustion process (3-4),
the volume is held constant and heat is released. The change in temperature is
given by
T4 = T3 + f * Q /cv
where Q is the heat released per pound of fuel which depends on the fuel,f is the fuel/air ratio for combustion which depends on several factors
associated with the design and temperature in the combustion chamber, and
cv is the specific heat at constant volume. From the
equation of state, we know that:
p4 = p3 * (T4 /T3)
During the
power stroke (4-5),
work is done by the gas on the piston. The expansion ratio is the
reciprocal of the compression ratio and we can use the same relations used
during the compression stroke:
p5 / p4 = r ^ (-gamma)
T5 / T4 = r ^ (1 - gamma)
Between stage 5 and stage 6, residual heat is
transferred
to the surroundings so
that the temperature and pressure return to the initial conditions of
stage 1 (or 2).
During the cycle,
work
is done on the gas by the piston between stages 2 and 3. Work is done by
the gas on the piston between stages 4 and 5. The difference between the work done by the
gas and the work done on the gas is shown in yellow and is the work produced
by the cycle.
We can calculate the work by determining the area enclosed
by the cycle on the p-V diagram.
But since the processes 2-3 and 4-5 are curves, this is a difficult
calculation.
We can also evaluate the work W by the difference of the heat into the gas
minus the heat rejected by the gas. Knowing the temperatures, this is an
easier calculation.
W = cv * [(T4 - T3) - (T5 - T2)]
The work times the rate of the cycle (cycles per second cps) is equal to
the
power P
produced by the engine.
P = W * cps
On this page we have
shown an ideal Otto cycle in which there is no heat entering (or
leaving) the gas during the compression and power strokes, no friction
losses, and instantaneous burning occurring at constant volume. In reality,
the ideal cycle does not occur and there are many losses associated with
each process. These losses are normally accounted for by efficiency factors
which multiply and modify the ideal result. For a real cycle, the shape
of the p-V diagram is similar to the ideal, but the area (work) is
always less than the ideal value.
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
