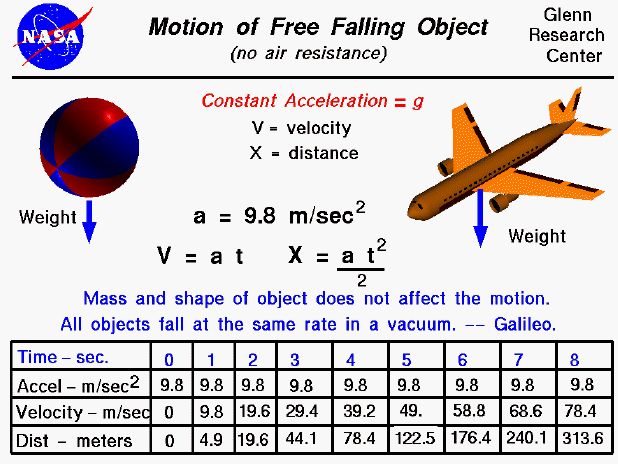

A text only version of this slide is available which gives the equations of motion and a tables with a solution to these equations.
An object that is falling through a vacuum is subjected to only one external force, the gravitational force, expressed as the weight of the object. An object that is moving only because of the action of gravity is said to be free falling and its motion can be described by Newton's Second Law of Motion. With algebra we can solve for the acceleration (change of velocity) of the object which is a constant and equal to the gravitational acceleration. The mass, size, and shape of the object are not a factor in describing the motion of the object; a beach ball falls at the same rate as an airliner. Knowing the acceleration, we can predict the velocity and location of a free falling object at any time using the equations shown in black on the slide. If the object were falling through the atmosphere, there would be an additional drag force acting on the object. And the physics involved with describing the motion of the object would be more complex.
In the table at the bottom, we show the acceleration, velocity, and location of a free falling object. Notice that the acceleration is a constant, the velocity increases linearly, and the location increases quadratically.
The remarkable observation that all free falling objects fall at the same rate was first proposed by Galileo, nearly 400 years ago. Galileo conducted experiments using a ball on an inclined plane to determine the relationship between the time and distance traveled. He found that the distance depended on the square of the time and that the velocity increased as the ball moved down the incline. The relationship was the same regardless of the mass of the ball used in the experiment. The story that Galileo demonstrated his findings by dropping two cannon balls off the Leaning Tower of Pisa is just a legend. However, if the experiment had been attempted, he would have observed that one ball hit before the other because falling cannon balls are not actually free falling - they are subject to air resistance and would fall at different terminal velocities.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov