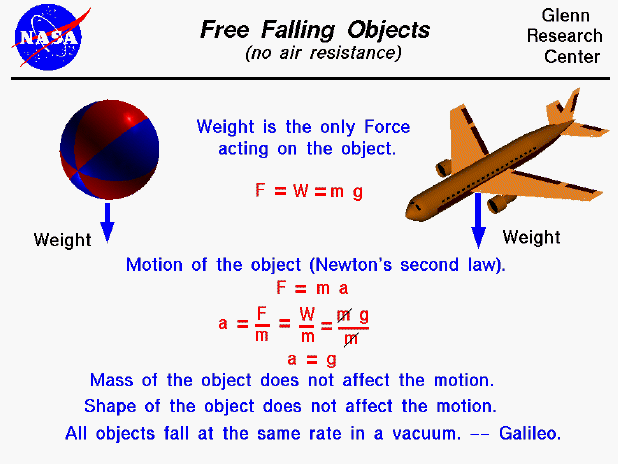

An object that is falling through a vacuum is subjected to only one external force, the gravitational force, expressed as the weight of the object. The weight equation defines the weight (W) to be equal to the mass of the object (m) times the gravitational acceleration (g), which is 9.8 meters per square second on the surface of the earth. The gravitational acceleration decreases with the square of the distance from the center of the earth. For many practical problems, we can assume this factor to be a constant. An object that is moving because of the action of gravity alone is said to be free falling. If the object were falling through the atmosphere, there would be an additional drag force acting on the object. And the physics involved with describing the motion of the object would be more complex.
The motion of a free falling object can be described by Newton's second law of motion, force (F) = mass (m) times acceleration (a). We can do a little algebra and solve for the acceleration of the object in terms of the net external force and the mass of the object ( a = F / m). The net external force is just the weight of the object (F = W). Substituting into the second law equation gives: a = W / m = m * g / m = g . The acceleration (change of velocity) of the object then becomes the gravitational acceleration. The mass, size, and shape of the object are not a factor in describing the motion of the object. So all objects, regardless of size or shape or mass (or weight) will free fall at the same rate; a beach ball will fall at the same rate as an airliner. Knowing the acceleration, we can predict the velocity and location of a free falling object at any time.
The remarkable observation that all free falling objects fall at the same rate was first proposed by Galileo, nearly 400 years ago. Galileo conducted experiments using a ball on an inclined plane to determine the relationship between the time and distance traveled. He found that the distance depended on the square of the time and that the velocity increased as the ball moved down the incline. The relationship was the same regardless of the mass of the ball used in the experiment. (The story that Galileo demonstrated his findings by dropping two cannon balls off the Leaning Tower of Pisa is just a legend.).
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov