Most general aviation or private airplanes are powered by
internal combustion engines
which turn
propellers to generate thrust.
The details of how a
propeller generates thrust is very
complex, but we can still learn a few of the fundamentals using the
simplified momentum theory presented here.
Propeller Propulsion System
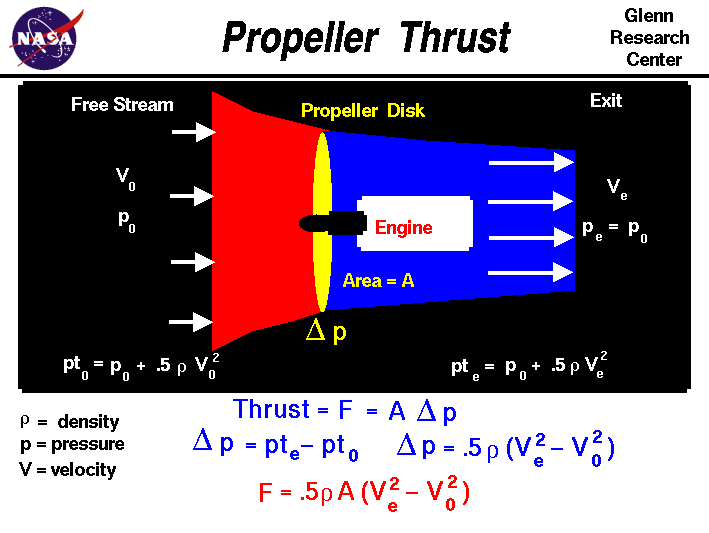
On the slide, we show a schematic of a propeller propulsion system
at the top and some of the equations that define how a propeller
produces thrust at the bottom. The details of propeller propulsion
are very complex because the propeller is like a rotating wing.
Propellers usually have between 2 and 6 blades. The blades are usually
long and thin, and a cut through the blade perpendicular to the long
dimension will give an airfoil shape. Because
the blades rotate, the tip moves faster than the hub. So to make the
propeller efficient, the blades are usually twisted. The angle
of attack of the airfoils at the tip is lower than at the hub because
it is moving at a higher velocity than the hub. Of
course, these variations make analyzing the airflow through the propeller a verydifficult task. Leaving the details to the aerodynamicists, let us
assume that the spinning propeller acts like a disk through which the
surrounding air passes (the yellow ellipse in the schematic).
The engine, shown in white, turns the propeller and does work on
the airflow. So there is an abrupt change in pressure across the
propeller disk. (Mathematicians denote a change by the Greek symbol
"delta" (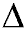 ).
Across the propeller plane, the pressure changes by "delta p"
( ).
Across the propeller plane, the pressure changes by "delta p"
(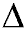 p). The
propeller acts like a rotating wing. From airfoil
theory, we know that the pressure over the top of a lifting wing
is lower than the pressure below the wing. A spinning propeller sets
up a pressure lower than free stream in front of the propeller and
higher than free stream behind the propeller. Downstream of the disk
the pressure eventually returns to free stream conditions. But at
the exit, the velocity is greater than free stream because the
propeller does work on the airflow. We can apply Bernoulli'sequation to the air in front of the propeller and to the air
behind the propeller. But we cannot apply Bernoulli's equation across
the propeller disk because the work performed by the engine violates
an assumption used to derive the equation. p). The
propeller acts like a rotating wing. From airfoil
theory, we know that the pressure over the top of a lifting wing
is lower than the pressure below the wing. A spinning propeller sets
up a pressure lower than free stream in front of the propeller and
higher than free stream behind the propeller. Downstream of the disk
the pressure eventually returns to free stream conditions. But at
the exit, the velocity is greater than free stream because the
propeller does work on the airflow. We can apply Bernoulli'sequation to the air in front of the propeller and to the air
behind the propeller. But we cannot apply Bernoulli's equation across
the propeller disk because the work performed by the engine violates
an assumption used to derive the equation.
Simple Momentum Theory
Turning to the math,
the thrust F generated by the propeller disk is equal to the
pressure jump delta p times the propeller disk area A:
F = delta p * A
A units check shows that:
force = (force/area) * area
We can use Bernoulli's equation to relate the
pressure and velocity ahead of and behind the propeller disk, but not through
the disk. Ahead of the disk the total pressure pt0 equals the
static pressure
p0 plus the dynamic pressure .5 * r * V0 ^2.
pt0 = p0 + .5 * r * V0 ^2
where r is the
air density
and V0 is the velocity of the aircraft.
Downstream of the disk,
pte = p0 + .5 * r * Ve ^2
where pte is the downstream total pressure and Ve is
the exit velocity.
At the disk itself the pressure jumps
delta p = pte - pt0
Therefore, at the disk,
delta p = .5 * r * [Ve ^2 - V0 ^2]
Substituting the values given by Bernoulli's equation into the
thrust equation, we obtain
F = .5 * r * A * [Ve ^2 - V0 ^2]
We still must determine the magnitude of the exit velocity. A
propeller analysis
based on the momentum equation provides this value.
Note that this thrust is an ideal number that does not
account for many losses that occur in practical, high speed
propellers, like tip losses. The losses must be determined by a more
detailed propeller theory, which is beyond the scope of these pages.
The complex theory also provides the magnitude of the pressure jump
for a given geometry. The simple momentum theory, however, provides a
good first cut at the answer and could be used for a preliminary
design.
Activities:
Guided Tours
Navigation ..

- Beginner's Guide Home Page
|
