Most general aviation or private airplanes are powered by
internal combustion engines
which turn
propellers to generate thrust.
The details of how a
propeller generates thrust is very
complex, but we can still learn a few of the fundamentals using the
simplified momentum theory presented here.
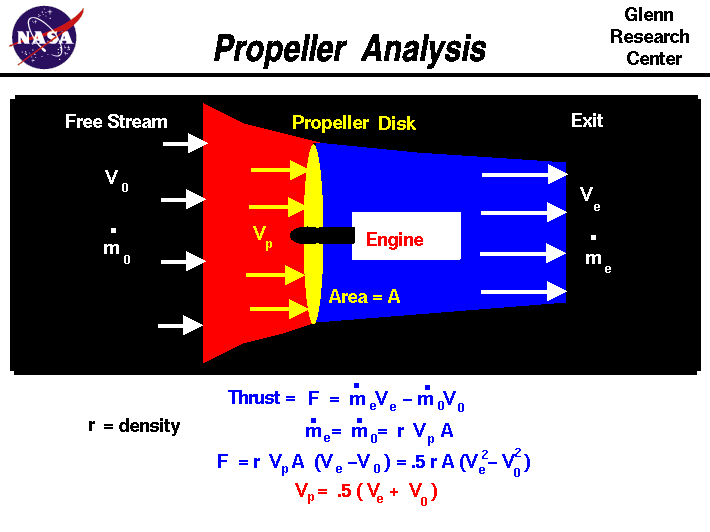
Propeller Propulsion System
On the slide, we show a schematic of a propeller propulsion system
at the top and some of the equations that define how a propeller
produces thrust at the bottom. The details of propeller propulsion
are very complex because the propeller is like a rotating wing.
Propellers usually have between 2 and 6 blades. The blades are usually
long and thin, and a cut through the blade perpendicular to the long
dimension will give an airfoil shape. Because
the blades rotate, the tip moves faster than the hub. So to make the
propeller efficient, the blades are usually twisted. The angle
of attack of the airfoils at the tip is lower than at the hub because
it is moving at a higher velocity than the hub. Of
course, these variations make analyzing the airflow through the propeller a verydifficult task. Leaving the details to the aerodynamicists, let us
assume that the spinning propeller acts like a disk through which the
surrounding air passes (the yellow ellipse in the schematic).
The engine, shown in white, turns the propeller and does work on
the airflow. So there is an abrupt change in pressure across the
propeller disk. The
propeller acts like a rotating wing. From airfoil
theory, we know that the pressure over the top of a lifting wing
is lower than the pressure below the wing. A spinning propeller sets
up a pressure lower than free stream in front of the propeller and
higher than free stream behind the propeller. Downstream of the disk
the pressure eventually returns to free stream conditions. But at
the exit, the velocity is greater than free stream because the
propeller does work on the airflow. We can apply Bernoulli'sequation to the air in front of the propeller and to the air
behind the propeller. But we cannot apply Bernoulli's equation across
the propeller disk because the work performed by the engine violates
an assumption used to derive the equation.
Simple Momentum Theory
Turning to the math, from the basic thrust
equation, we know that the amount of thrust
depends on the mass flow rate through the
propeller and the velocity change through the propulsion system. Let us
denote the free stream conditions by the subscript "0", the conditions at
the propeller by the subscript "p", and the exit conditions
by the subscript "e". The thrust F is equal to the mass flow rate m dot
times the difference in velocity V.
F = [m dot * V]e - [m dot * V]0
There
is no pressure-area term because the pressure at the exit is equal to the
free stream pressure.
The mass flow through the
propulsion system is a constant, and we can determine the value at
the plane of the propeller. Since the propeller rotates, we can
define an area A that is swept out by the propeller of blade length
L. Through this area, the mass flow rate is
density r
times velocity Vp,
times area.
m dot = r * Vp * A
Substitute this value for the mass flow rate into the thrust equation to get thethrust in terms of the exit velocity, entrance velocity, and velocity
through the propeller.
F = r * Vp * A * [Ve - V0]
On
another page,
we have determined that the thrust is related to the pressure jump
across the propeller disk. Using
Bernoulli's equation
upstream and downstream of the propeller, we obtain:
F = .5 * r * A * [Ve ^2 - V0 ^2]
Combining the two expressions for the the thrust F and solving for Vp;
Vp = .5 [Ve + V0]
The airspeed through the propeller disk
is simply the average of the free stream and exit velocities.
Note that this thrust is an ideal number that does not
account for many losses that occur in practical, high speed
propellers like tip losses. The losses must be determined by a more
detailed propeller theory, which is beyond the scope of these pages.
The complex theory also provides the magnitude of the pressure jump
for a given geometry. The simple momentum theory, however, provides a
good first cut at the answer and could be used for a preliminary
design.
Activities:
Guided Tours
Navigation ..

- Beginner's Guide Home Page
|
