 |
 |
+
Text Only Site
+ Non-Flash Version
+
Contact Glenn |
|
|

|
Getting a Little "Lift" out of Calculus Part
I: Answers
|

|
- When I printed out the enlarged picture of the plotter view
panel, I found the curve to cover 6.5 cm. Because of this, I
divided it into 12 rectangles with width .5 cm each (see
Figure 1). I then took
the height measurements of each rectangle and recorded them in a
spreadsheet (see Table
1).
- The program displays the plot from 0 to 1 square foot, so I
converted the X-axis to (0 to 144) square inches. I then divided the
displayed 144 inches by the measured 6.5 cm to find an
X-scaling factor of
22.15. On the Y-axis, 1.0 psi was equivalent to 6.0 cm,
which gives the Y-scaling factor of
.1666. On the spread sheet, I have multiplied by the
approtiate scaling factors.
- I then multiplied
the scaled values to find the total area under the curve. This
gave a value of 68.4
lbs which represented the lift force.
- I found the following functions to represent the curves (shown
in Figure
2):
f1(x) = 14.81
f2(x) = .0065 x + 13.87
- I finished by solving the following integral:
|
Integral (X=0 to X=144) [f1(x) - f2(x)] dx
|
|
135.3 - 66.3 = 69.0
lbs
|
- The value calculated by FoilSim is
66 lbs, so both
answers compare favorably.
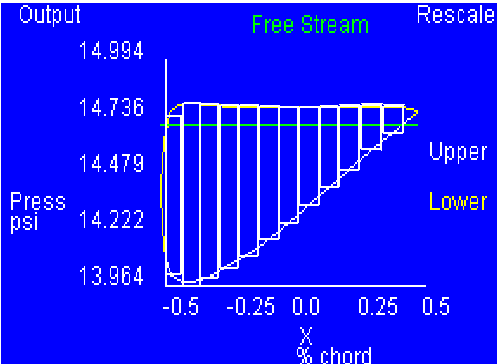 Figure 1
Figure 1
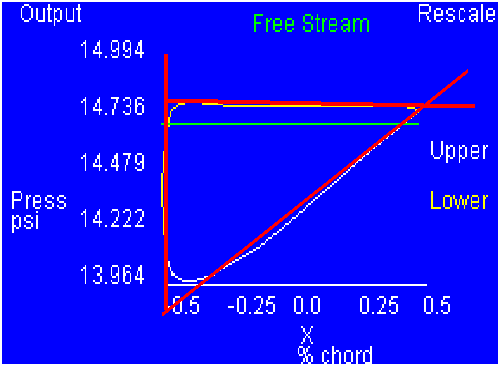 Figure 2
Figure 2
Table 1
|
|
Measured
|
|
Scaled
|
|
|
|
Rectangle
|
Width (cm)
|
Height (cm)
|
Width (sq. in.)
|
Height (lbs/sq. in.)
|
Area (lbs)
|
|
1
|
0.50
|
4.2
|
11.07
|
.7
|
7.7
|
|
2
|
0.50
|
5.0
|
11.07
|
.83
|
9.2
|
|
3
|
0.50
|
4.6
|
11.07
|
.766
|
8.5
|
|
4
|
0.50
|
4.4
|
11.07
|
.733
|
8.1
|
|
5
|
0.50
|
4.1
|
11.07
|
.683
|
7.5
|
|
6
|
0.50
|
3.6
|
11.07
|
.6
|
6.6
|
|
7
|
0.50
|
3.1
|
11.07
|
.516
|
5.7
|
|
8
|
0.50
|
2.6
|
11.07
|
.433
|
4.8
|
|
9
|
0.50
|
2.1
|
11.07
|
.35
|
3.9
|
|
10
|
0.50
|
1.7
|
11.07
|
.283
|
3.1
|
|
11
|
0.50
|
1.1
|
11.07
|
.183
|
2.0
|
|
12
|
0.50
|
.7
|
11.07
|
.117
|
1.3
|
|
|
|
|
|
|
|
|
|
|
|
|
Total (in lbs)
|
68.4
|
|
Related Pages:
Standards
Activity
Worksheet
Lesson Index
Aerodynamics Index
|
|
|
