
Air is a gas, and a very important property of any gas is the speed of sound through the gas. Why are we interested in the speed of sound? The speed of "sound" is actually the speed of transmission of a small disturbance through a medium. (Sound itself is a sensation created in the human brain in response to sensory inputs from the inner ear, which is sensitive to variations in pressure. We won't comment on the old "tree falling in a forest" discussion!)
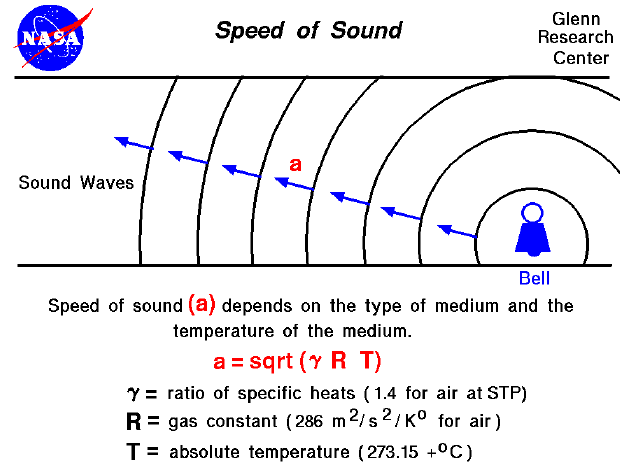
The speed of sound depends on the state of the gas--more specifically, the square root of the temperature of the gas. The speed of sound (a) is equal to the square root of the ratio of specific heats (g) times the gas constant (R) times the absolute temperature (T).
a = sqrt [g * R * T]
The derivation of this equation is given on a separate page. Notice that the temperature must be specified on an absolute scale (Kelvin or Rankine). The speed of sound depends on the temperature, and temperature changes with altitude in a very complex way. Engineers have created a mathematical model of the atmosphere to account for the effects of altitude on the temperature. Here's a Java program that you can use to study the effect of altitude on the speed of sound.
To change input values, click on the input box (black on white), backspace over the input value, type in your new value, and hit the Enter key on the keyboard (this sends your new value to the program). You will see the output boxes (yellow on black) change value. You can use either English or Metric units and you can input either the Mach number or the speed by using the menu buttons. Just click on the menu button and click on your selection.
As an object moves through the air, or air is forced to move through a device, the air is disturbed. The disturbances are transmitted through the air at the speed of sound. (You can study how these disturbances are transmitted with another interactive sound wave simulator.) If the object moves much slower than the speed of sound, conditions are said to be subsonic, and compressibility effects are small and can be neglected. If the object moves up to four times faster than the speed of sound, the conditions are said to be supersonic, and compressibility effects (like shock waves) are present in the gas. If the object moves near the speed of sound, conditions are said to be transonic, and other compressibility effects (like flow choking) become important. If the object moves more than five times the speed of sound, conditions are said to be hypersonic, and the high energy involved under these conditions has significant effects on the air itself. The important parameter in each of these situations is the ratio of the speed of the object to the speed of sound. Aeronautical engineers call this ratio the Mach number. A Mach number less than one indicates subsonic flow, a Mach number near one is transonic, and a Mach number greater than one is supersonic or hypersonic.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov