
Math & Science Home | Proficiency Tests | Mathematical Thinking in Physics | Aeronauts 2000
The
Transcendentality of 
By definition,
the number
is the ratio of the circumference to the diameter of a circle. This ratio
is the same for all circles.
is an irrational number. It cannot be represented as the ratio of two
integers, regardless of the choice of integers. Equivalently, it cannot
be represented as an unending, periodic decimal.
is also a transcendental number. It is not a root of any algebraic
equation of the form
where
the ai are all rational numbers and n is finite. For comparison,
is also an irrational number. But
is not transcendental since it is a root of the equation
Both
and
are irrational, but only
is transcendental. What makes the difference? One important argument is
that a line of length
can be constructed using classical techniques (i.e., using compass
and straight-edge in a finite number of steps). But, because of the way
is defined, a line of length
cannot be so constructed. (A curve can. Mark off a unit
segment. Bisect the segment. Using the midpoint as center, scribe the
appropriate circle. The circle has length
.)
To illustrate,
let us first consider .
To make a construction that produces a line of this length, we begin with
two unit-length segments placed end to end so that one segment is at right
angles with the other. We then, connect the free ends to complete a right
triangle. The new line has length
Now,
consider .
A circle of unit diameter has its circumference =
.
Draw a unit circle, and locate its center. From the center produce a set
of n radial lines each separated from its neighbor by an angle 2
/n.
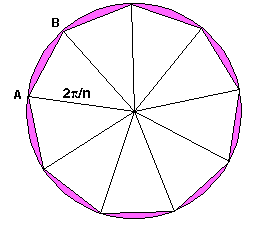
Approximation for n = 9
![]()
Isoseles Triangle
Now, connect the ends with straight line segments to form a set of isosceles triangles. The sum of the lengths of these straight-line segments approaches the circumference of the circle as n approaches infinity (see figure for n = 9).
To construct
a line of length ,
we have but to produce the length AB n times along any line. In the figure,
n = 9, AB is a typical straight line segment completing an isosceles triangle,
and Circumference
![]() 9(AB) (see figure).
9(AB) (see figure).
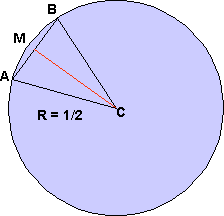
Now, let us use some algebra to calculate the length AB in the general case. We begin by redrawing part of our previous picture.
One isosceles
triangle (![]() ABC
with one vertex at the center C and two more vertices on the circle at
A and B) is selected (see figure). The angle subtended at C is 2
ABC
with one vertex at the center C and two more vertices on the circle at
A and B) is selected (see figure). The angle subtended at C is 2/n.
We wish to calculate the length AB, and then to estimate how good an approximation
the value n(AB) is to the actual circumference of the circle.
The line
CM bisects the angle 2/n,
and meets the line AB at right angles. Thus, the triangle CMA is a right
triangle, and the length AM = ½(AB).
AM = ½ sin (
/n)
&
AB = sin (/n).
Finally,
n(AB) = n sin (/n).
Since
the actual circumference of the circle is ,
we now write
=
{(sin (
/n))/(
/n)}
=
{(sin (
))/(
)}
where
=
/n.
The value
n(AB) differs from
by the multiplicative factor (sin (
))/(
),
with
=
/n.
Notice that, in the limit as n
,
0 and (sin (
))/(
)
1. The value n(AB) does indeed approach
in the limit. But, while the limit exists, the actual
function f(
)
= (sin (
))/(
)
does not exist at
= 0. It becomes the indeterminate form 0/0. Thus, although n(AB)
may approach the actual circumference to any arbitrary precision we might
desire, the actual value n(AB) =
can never be obtained from any construction of the type outlined above.
Please send suggestions/corrections to:
Web Related: David.Mazza@grc.nasa.gov
Technology Related: Joseph.C.Kolecki@grc.nasa.gov
Responsible NASA Official: Theresa.M.Scott (Acting)