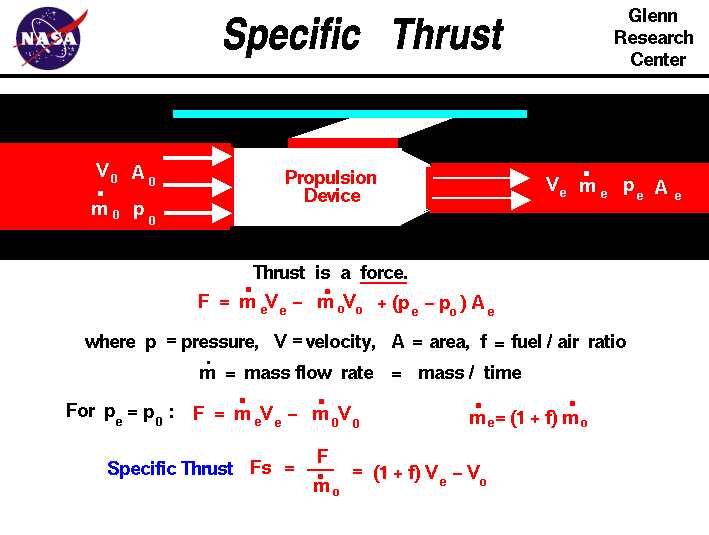
Thrust is the force which moves an
aircraft through the air. Thrust is generated by the engines of the
airplane through the reaction of
accelerating a mass of gas. The gas is accelerated to the the rear
and the engine and aircraft are accelerated in the opposite
direction. To accelerate the gas, we need some kind of propulsion
system. We will discuss the details of various propulsion systems
on some other pages. For right now, let us just think of the
propulsion system as some machine which accelerates a gas.
From Newton's second law of motion, we
can define a force to be the change in momentum of an object with a
change in time. Momentum is the object's mass times the
velocity. When dealing with a gas, the general thrust
equation is given as:
F = mdot e * Ve - mdot 0 * V0 + (pe - p0) * Ae
Thrust F is equal to the exit mass flow rate
mdot e times the exit velocity Ve minus the
free stream mass flow rate mdot 0 times
the free stream velocity V0 plus the pressure difference across the
engine (pe - p0) times the engine area Ae.
For gas
turbine engines, the nozzle is usually
designed to make the exit pressure equal to free stream. In that case
the thrust equation simplifies to:
F = mdot e * Ve - mdot 0 * V0
We further note that
the exit mass flow rate is equal to the incoming mass flow rate plus
the fuel flow rate. Using the fuel to air
mass flow ratio f, we obtain:
mdot e = (1 + f) * mdot 0
Now using a little algebra, we can define a new
variable called the specific thrust Fs which depends only on
the velocity difference produced by the engine:
F / mdot 0 = Fs = (1 + f) * Ve - V0
A "specific" property does not
depend on the mass of that property. We can easily compute the exit
velocity if we know the engine pressure ratio
EPR, the engine temperature ratio ETR,
and the nozzle performance. The EPR and
ETR depend on the component pressure and temperature ratios which are
given on each of the component thermodynamic slides. With this
information, we can easily compute the thrust
of a gas turbine engine.
Why are we interested in specific thrust? First, it is an
indication of engine efficiency. Two different engines have
different values of specific thrust. The engine with the higher value
of specific thrust is more efficient because it produces more thrust
for the same amount of airflow. Second, it simplifies our
mathematical analysis of
turbine engine thermodynamics.
The math
concerning work and energy contains the mass flow rate as a
multiplier. We could carry it along, but since the mass flow rate is
a constant, the math is easier if we just divide it out at the
beginning and put it back in at the end. Third, it gives us an easy
way to "size" an engine during preliminary analysis. The result of
our thermodynamic analysis is a certain value of specific thrust. The
aircraft drag defines the required value of thrust. Dividing the
thrust required by the specific thrust tells us how much airflow
our engine must produce and this determines the physical size of the
engine.
There is a similar efficiency parameter called the
specific impulse
which is used to characterize rocket engine performance.
Activities:

Guided Tours
-
 Thrust Equation:
Thrust Equation:

Navigation ..

- Beginner's Guide Home Page
|
