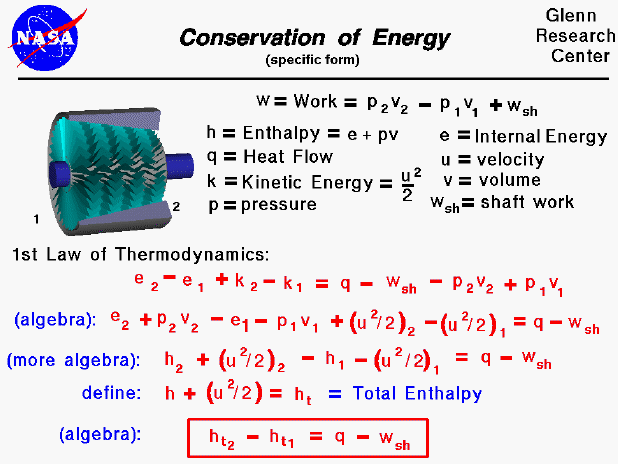

The conservation of energy is a fundamental concept of physics along with the conservation of mass and the conservation of momentum. Within some problem domain, the amount of energy remains constant and energy is neither created nor destroyed. Energy can be converted from one form to another (potential energy can be converted to kinetic energy) but the total energy within the domain remains fixed. On some separate slides, we have discussed the state of a static gas, the properties which define the state, and the first law of thermodynamics as applied to any system, in general. On this slide we derive a useful form of the energy conservation equation for a gas beginning with the first law of thermodynamics.
Thermodynamics is a branch of physics which deals with the energy and work of a system. As mentioned on the gas properties slide, thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. As aerodynamicists, we are most interested in thermodynamics in the study of propulsion systems and understanding high speed flows.
Aeronautical engineers usually simplify a thermodynamic analysis by using intensive variables; variables that do not depend on the mass of the gas. We call these variables specific variables, and many of the state properties listed on this slide, such as the work, internal energy, and volume are specific quantities. Engineers usually use the lower case letter for the "specific" version of a variable. There are two parts to the specific work for a moving gas. Some of the work, called the shaft work (wsh) is used to move the fluid or turn a shaft, while the rest of the work goes into changing the state of the gas. The specific internal energy is a state variable defined by the first law of thermodynamics. A useful additional state variable for a gas is the specific enthalpy of the gas, as shown on the slide. There are two additional terms added to the standard first law of thermodynamics for a moving gas and these involve the specific kinetic energy of the gas (k). (If we were dealing with a large amount of gas, we would also have to include some terms for potential energy, but we are neglecting those effects here.)
If we perform a little algebra on the first law of thermodynamics, we can begin to group some terms of the equations. In particular, the enthalpy of the gas can be used to simplify the equation. By combining the velocity terms with the enthalpy terms to form the total specific enthalpy we can further simplify the equation. The total specific enthalpy is analogous to the total pressure in Bernoulli's equation; both expressions involve a "static" value plus one half the square of the velocity.
The final, most useful, form of the energy equation is given in the red box. For a compressor or power turbine, there is no external heat flow into the gas and the "q" term is set equal to zero. In the burner, no work is performed and the "wsh" term is set to zero.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov