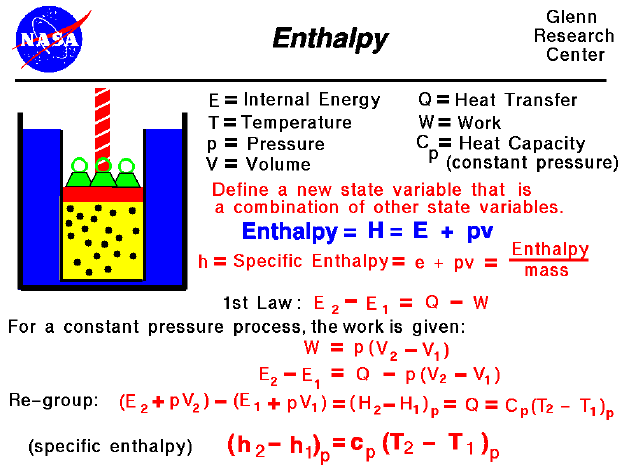
Thermodynamics is a branch of physics which deals with the energy and work of a system. As mentioned on the gas properties slide, thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. As aerodynamicists, we are most interested in thermodynamics in the study of propulsion systems and understanding high speed flows.
The state of a gas is defined by a several properties including the temperature, pressure, and volume which the gas occupies. From our study of the first law of thermodynamics, we have found that the internal energy of a gas is also a state variable, that is, a variable which depends only on the state of the gas and not on any process that produced that state. We are free to define additional state variables which are combinations of existing state variables. These new variables will often make the analysis of a system much simpler. For a gas, a useful additional state variable is the enthalpy (H) which is defined to be the sum of the internal energy (E) plus the product of the pressure (p) and volume (V),
H = E + p * V
The enthalpy can be made into an intensive, or "specific" , variable by dividing by the mass. Propulsion engineers use the specific enthalpy in engine analysis more than the enthalpy itself.
How does one use this new variable called enthalpy? Let's consider the first law of thermodynamics for a gas. For a system with heat transfer (Q) and work (W), the change in internal energy is equal to the difference in the heat transfer into the system and the work done by the system:
Equation 1 : E2 - E1 = Q - W
The work and heat transfer, in general, depend on the process. For the special case of a constant pressure process, the work done by the gas is given as the constant pressure (p) times the change in volume (V):
Equation 2: W = p * [V2 - V1]
Substituting into the first equation, we have
Equation 3: E2 - E1 = Q - p * [V2 - V1]
Let's group the conditions at state 2 and the conditions at state 1 together:
Equation 4: (E2 + p * V2) - (E1 + p * V1) = Q
The (E + p * V) can be replaced by the enthalpy (H).
Equation 5: H2 - H1 = Q
From our definition of the heat transfer, we can represent Q by some heat capacity coefficient (Cp) times the temperature (T).
Equation 6: (H2 - H1)p = Cp (T2 - T1)p
We have enclosed the terms of the equation in parentheses with a "p" subscript to remind ourselves that this equation is only true for a constant pressure process. At the bottom of the slide, we have divided by the mass of gas to produce the specific enthalpy equation version. The specific heat capacity (cp) is called the specific heat at constant pressure and is related to the universal gas constant of the equation of state. This final equation is used to determine values of specific enthalpy for a given temperature. The enthalpy is also used in the evaluation of the work done on the flow by a compressor or the work available from a power turbine.
Thermodynamics:
Calculating Fuel Flow Rate:
Compressor:
Power Turbine:
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov