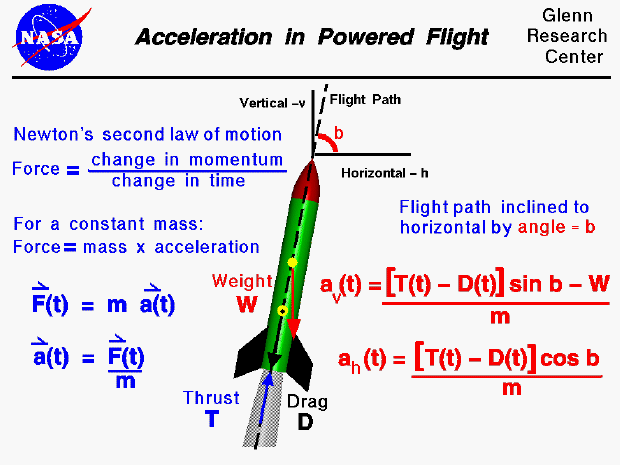

The forces on a model rocket change dramatically in both magnitude and direction throughout a typical flight. This figure shows the accelerations on a rocket during the powered portion of the flight, following liftoff. The acceleration is produced in response to Newton's first law of motion. A net external force is being applied to the rocket. During the powered portion of the flight, the rocket is subjected to the forces of weight, thrust, and drag.
The acceleration of a powered model rocket is described by Newton's second law of motion. In general, Newton's law prescribes that the force on an object (F) is equal to the change in momentum (mass times velocity) per unit time. If we assume that the mass is constant, the equation becomes the more familiar force equals mass (m) times acceleration (a). (F = m * a) The force and acceleration are vector quantities having both a magnitude and a direction while the mass is a scalar and has only a magnitude. (Mathematicians will often denote a vector with a small arrow over the symbol). For the model rocket, the thrust (T) and drag (D) forces change with time (t). To denote that thrust, drag, and therefore the acceleration, are all functions of time we include the "(t)" symbol next to these variables. Newton's second law is then written as [ F(t) = m * a(t) ]. We can use algebra to solve for the accelerations: [ a(t) = F(t) / m ].
Under ideal conditions, the flight path of the model rocket would be perfectly vertical. In practice, the flight path is inclined due to the action of the wind. The angle which the flight path makes with the horizontal is called the inclination angle (b). If we consider the forces in the vertical (v) and horizontal (h) directions, we obtain two equations for the acceleration; one for the vertical and one for the horizontal. The "cos b" and "sin b" are the trigonometric functions cosine and sine of the inclination angle. The vertical acceleration is given by the following equation: ( av(t) = ( [T(t) - D(t)] * sin b - W ) / m ). The horizontal acceleration is give by: ( ah(t) = ( [T(t) - D(t)] * cos b ) / m ). If the flight path was perfectly vertical, the inclination angle would be 90 degrees. The cosine of 90 degrees is zero, so the horizontal acceleration would be zero. The sine of 90 degrees is 1.0, so the vertical acceleration would equal the thrust minus the drag minus the weight divided by the mass.
To make a rocket fly as high as possible, we want the vertical acceleration to be as high as possible. Considering the acceleration equations, this tells us that we want the inclination angle to be 90 degrees, the thrust to be high, the drag low, and the weight low. Anything that we can do to the model rocket design to accomplish these four goals will improve the performance of the rocket.
Notice that for a model rocket, the weight of the propellant is small relative to the weight of the entire vehicle. So, in determining the acceleration we can assume that the weight (or mass) remains nearly constant. This is different from a full scale rocket in which the propellants represent a large portion of the weight of the vehicle. Changes in the weight (mass) of the propellant must then be included in any determination of velocity or acceleration during the flight. The equations shown on this slide would not be valid for a full scale rocket.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov