
An interactive Java applet that demonstrates the information found on this slide is also available. The applet presents problems that you can solve using the range equation.
As discussed on the airplane cruise slide, an airplane can sustain a constant speed and level flight, in which the lift is equal to the weight, and the thrust is equal to the drag. Since there is no net external force on the aircraft, the aircraft will maintain a constant airspeed as described by Newton's First Law of Motion. However, if the forces become unbalanced, the aircraft will move in the direction of the greater force.
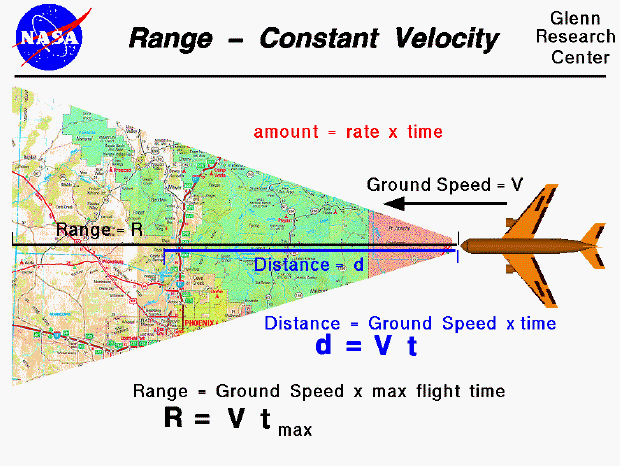
If we take into account the relative velocity of the wind, we can determine the ground speed of a cruising aircraft. The ground speed remains constant as long as the wind speed is constant. Assuming a constant ground speed, we can use a simple rate equation to determine how far a cruising aircraft will fly in a given span of time. The general rate equation is an amount is equal to the rate times the time. The amount is the distance (d) the airplane has flown, the rate is the aircraft's ground speed (V), and the time is the time (t) aloft. Our general rate equation then becomes a distance equation: the distance flown is equal to the ground speed times the time aloft.
d = V * t
Airplanes (unfortunately) cannot stay in the air forever. There is a time limit, or maximum time, that an airplane can stay aloft, which is usually determined by the fuel. When the airplane runs out of fuel, the engine stops. The drag then slows the airplane, which decreases the lift and, eventually, the airplane comes back to earth. The maximum distance that the aircraft can fly is equal to the ground speed times the maximum time (t max). We call this distance the maximum range (R) of the aircraft.
R = V * t max
The maximum flight time depends on how much fuel is carried by the aircraft and how fast the fuel is burned. A summary of information needed to determine the range is given on a separate page.
(On this page, we have taken a very simple view of aircraft range--for academic purposes. In reality, calculating the range is a complex problem because of the number of variables. An aircraft's flight is not conducted at a single ground speed but varies from zero (at takeoff) to cruise conditions and back to zero (at landing). Extra fuel is expended in climbing to altitude and in maneuvering the aircraft. The weight constantly changes as fuel is burned. So the lift, drag, and thrust (fuel consumption rate) also continually change. On real aircraft, as with your automobile, there is usually a fuel reserve; and the pilot makes sure to land the plane with fuel still on board.)
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov