
An interactive Java applet that demonstrates the information found on this slide is also available. The applet presents problems that you must solve by using the range equation.
Aircraft Range
An airplane can cruise at a
constant speed and level flight in which the lift is equal to the
weight, and the thrust is equal to the drag. Since there is no net
external force on the aircraft, the
aircraft will maintain a constant airspeed, as described by Newton's
first law of motion. The distance that the
aircraft can fly is then given by a simple rate equation:
distance equals velocity times time
aloft. The maximum distance that the airplane can fly is
called the range.
Maximum Time Aloft
Airplanes (unfortunately) cannot stay in the air forever. There is a
time limit, or maximum time, that an airplane can stay aloft; and the
time limit is usually determined by the amount of fuel. When the
airplane runs out of fuel, the engine stops. Drag then slows the
airplane, decreasing the lift. Eventually the airplane comes back to
earth. We can determine maximum time available using the rate
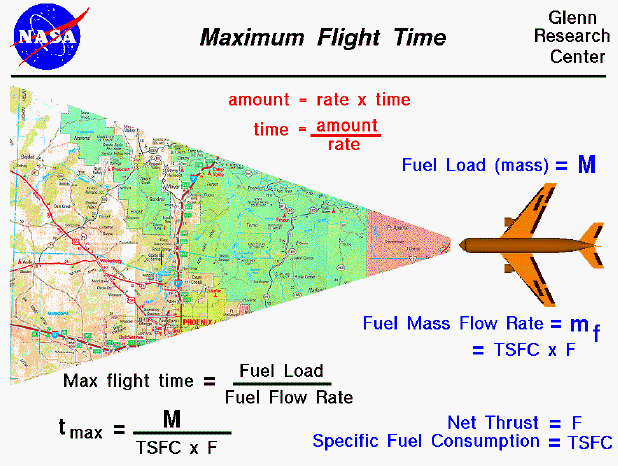
equation. The amount is equal to the rate
times the time. If we do a little algebra, we can rearrange the
equation to solve for the time. Time equals the amount of fuel that we
have divided by the rate that the fuel is being burned. The amount of fuel
is called the fuel load and is denoted by M (given in
units of kilograms or pounds mass). The rate at which the fuel is
being burned is the
fuel mass flow rate
(given in kilograms
per hour or pounds mass per hour and denoted by mf).
The maximum flight time (t max) is then equal to the fuel load divided
by the fuel mass flow rate (t max = M / mf ).
The fuel mass flow rate depends on
the type of engine used and the throttle setting chosen by the pilot.
The fuel mass flow rate is related to the thrust (F) by a factor called
the specific fuel consumption (TSFC). The
specific fuel consumption equals the mass flow rate divided by the thrust.
(TSFC = mf / F ). Again using algebra, (mf = TSFC * F )
Collecting all
this information, we arrive at the final equation.
The maximum time aloft is equal to the fuel
load divided by the specific fuel consumption times the
thrust (t max = M / (TSFC * F)).
A summary of information needed to determine the
range is given on a separate page.
Aircraft Design
What does this tell us? Obviously, if we carry more
fuel we can fly longer (in time) and farther (in distance) than if we
carried less fuel. If our engine has a low specific fuel consumption
we can also fly longer. Turboprop and
turbofan engines have low specific fuel
consumption and are used on long range airliners. If we can run the
engine at a low throttle setting, producing a minimum amount of
thrust we can also fly longer. But we must produce enough thrust to
equal drag in a cruise condition. Aircraft with a low drag, or a high
L/D ratio, require less thrust and can fly
longer and farther than aircraft with a low L/D ratio.
Aerodynamicists try to design aircraft with high L/D ratios and
engines with low specific fuel consumption.
NOTE: On this page, we have taken a very simple view of aircraft range - for academic purposes. In reality, calculating the range is a complex problem because of the number of variables. An aircraft's flight is not conducted at a single ground speed but varies from zero (at takeoff) to cruise conditions and back to zero (at landing). Extra fuel is expended in climbing to altitude and in maneuvering the aircraft. The weight constantly changes as fuel is burned; so the lift, drag, and thrust (fuel consumption rate) also continually change. (On real aircraft, just like with your automobile, there is usually a fuel reserve. The pilot makes sure to land the plane with fuel still on board.)
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov