
A text only version of this slide is available which gives all of the flow equations. An interactive Java applet is also available which solves the various equations shown here.
As an object moves through a gas, the gas molecules are deflected around the object. If the speed of the object is much less than the speed of sound of the gas, the density of the gas remains constant and the flow of gas can be described by conserving momentum and energy. As the speed of the object increases towards the speed of sound, we must consider compressibility effects on the gas. The density of the gas will vary locally as the gas is compressed by the object.
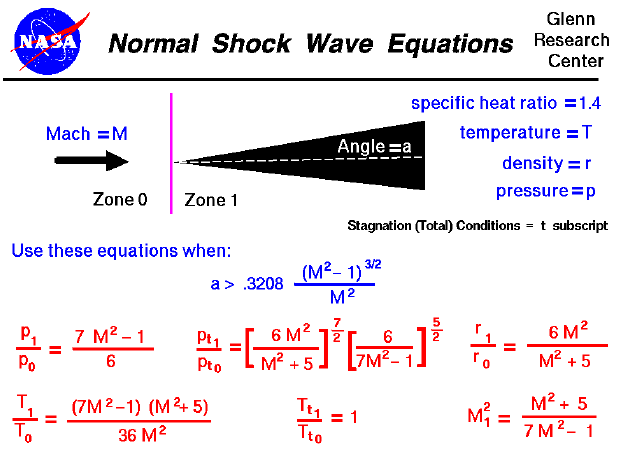
For compressible flows with little or small flow turning, the flow process is reversible and the entropy is constant. The change in flow properties are then given by the isentropic relations (isentropic means "constant entropy"). But when an object moves faster than the speed of sound, and there is an abrupt decrease in the flow area, the flow process is irreversible and the entropy increases. Shock waves are generated which are very small regions in the gas where the gas properties change by a large amount. Across a shock wave, the static pressure, temperature, and gas density increases almost instantaneously. Because a shock wave does no work, and there is no heat addition, the total enthalpy and the total temperature are constant (the ratio of Tt1 to Tt0 is equal to one). But because the flow is non-isentropic, the total pressure downstream of the shock is always less than the total pressure upstream of the shock; there is a loss of total pressure associated with a shock wave. The ratio of the total pressure is shown on the slide. Because total pressure changes across the shock, we can not use the usual (incompressible) form of Bernoulli's equation across the shock. The Mach number and speed of the flow also decrease across a shock wave.
If the shock wave is perpendicular to the flow direction it is called a normal shock. On this slide we have listed the equations which describe the change in flow variables for flow across a normal shock. The equations presented here were derived by considering the conservation of mass, momentum, and energy. for a compressible gas while ignoring viscous effects. The equations have been further specialized for a one-dimensional flow without heat addition and for a gas whose ratio of specific heats is 1.4 (air). The equations can be applied to the two dimensional flow past a wedge for the combination of free stream Mach number and wedge angle listed in blue. If the wedge angle is less than the angle shown on the slide, an attached oblique shock occurs and the equations are slightly modified.
The equations describing oblique and normal shocks and isentropic flows were published in a NACA report (NACA-1135) in 1951.
Navigation..
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov