
 |
|
Glenn
|
This page shows the mathematical derivation of the isentropic flow equations beginning with the definition of the gas constant from the equation of state and using information from the entropy slide. A text version of this slide is also available.

We can determine the value of the constant in Equation 13, by defining the total conditions to be the pressure and density when the flow is brought to rest isentropically. We then obtain the other forms of this relation, which are shown on the isentropic flow equation slide.
The second derivation involves determining the relation between the static and total conditions for an isentropic flow in terms of the Mach number. In this derivation, we use the information from the enthalpy equation.
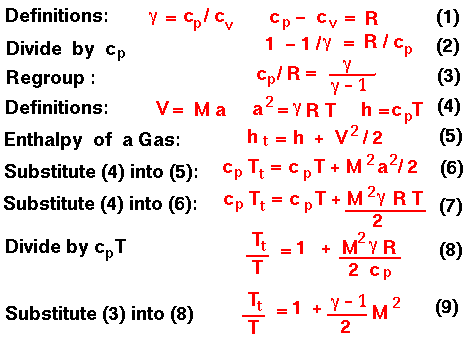
Equation 9 can be inverted to give the form on the isentropic flow slide. Using the previously derived results for pressure and density for an isentropic flow and the equation of state, all other forms can be easily derived.
Go to...
byTom
Benson
Please send suggestions/corrections to: benson@grc.nasa.gov