|
|
Trimmed
Aircraft Equations
Answers
- Solve the trimmed
aircraft equation for T, the lift due to the tail, using the following
data:
W = 18,000 kg,
dw= 2.4 m, dt = 18.3 m, T
= -2361 kg.
Notice the sign of the tail lift. In which direction does this tail
lift act? It acts downward.
- Now suppose we
use a B17G
aircraft (http://en.wikipedia.org/wiki/B-17_Flying_Fortress)
as our problem model. Assuming 100 kg has been used for fuel, the weight
of the B17G is the takeoff weight less 100 kg = 32,620
kg.
- We are now going
to use the following assumptions for the values of wing lift and distance
from the wing to the center of gravity (cg): W = 35,470 kg, dw
= 1.07 m. Using our trimmed aircraft equation and the fact that the
total lift is equal to the sum of the wing lift and the tail lift, we
have two simultaneous linear equations: L= W + T and (W x dw)
+ (T x dt) = 0. Remembering that the total lift is necessarily
equal to our total weight (from Problem 2 above), we can solve our first
equation for the tail lift, T = -2850 kg.
- Substituting T,
W, and dW into our second equation, solve for dt.
dt = 13.3 m.
- Now let's assume
something in our B17G shifts position, such that the cg moves 0.5 m
aft. Then dw becomes 0.57 m and dt becomes 12.8
m. So, to trim the plane for a fixed wing lift, our value of tail lift
must now be changed.
Using the second equation, T becomes -1580
kg.
What change is necessary in tail lift due to the 0.5 m change in cg?
1270 kg change.
From our Trimmed Aircraft slide, we realize our altitude will change
because the total lift has changed. What is the direction of the altitude
change? The altitude increases.
- Now please read
the slide called Size Effects
in Airplane Aerodynamics. Given that the total lift is directly proportional
to the total wing and tail area, we can write an equation W + T = k(Aw
+ At), where Aw is the area of the wing, At
is the area of the tail, and W and T are, as before, the lifts due to
the wing and tail, and k represents a constant (which includes the lift
coefficient and other aerodynamic parameters which we assume to be held
constant). We can also say that the lift due to the wing is proportional
to the area of the wing and likewise for the tail, resulting in the
equations: W = kw Aw and T = kt At.
Because the conditions determining these constants are the same at any
given time, let us allow kw = kt = k. From our
B17G data, we know Aw, which coupled with W given in Problem
3, enables us to find k = 250 kg/m2.
- Now that we know
k, let's use the tail lift which you found in Problem 3 to determine
the area of the tail, i.e., At = abs
T/k, = 11.4 m2. We can see that the
area of the tail is signigicantly smaller than the area of the wing.
Why does this make sense? Because dt
is relatively large compared to dw, At is
proportionally smaller than Aw.
- An interesting,
but simple, matrix problem involves adding a third equation to our trimmed
aircraft system. For a relatively short time period, we can fix the
aircraft weight. The three simultaneous linear equations are: L = 32,620
kg; L - W - T = 0; and W x dw + T x dt = 0. Substitute
in the coefficients dw and dt from Problems 3
and 4, and rewrite the system as a matrix equation.
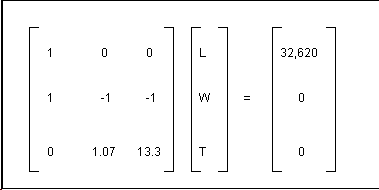
- Using your graphing
calculator, find the inverse of the coefficient matrix.
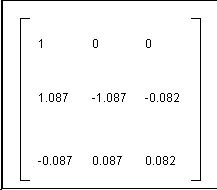
- Multiply both sides
of the matrix equation on the left by the inverse matrix and simplify.
Therefore, L = 32,620 kg, W= 35,474
kg, T = -2854 kg.
Compare these answers with those assumed for L in Problem 2, and calculated
for W and T in Problem 3. Do they agree? Yes!
|
