To better understand certain problems involving aircraft
and propulsion
it is necessary to use some mathematical ideas from
trigonometry, the study of triangles.
Most people are introduced to trigonometry in high school.
There are many complex parts to trigonometry, but on this page
we are concerned chiefly with definitions and terminology.
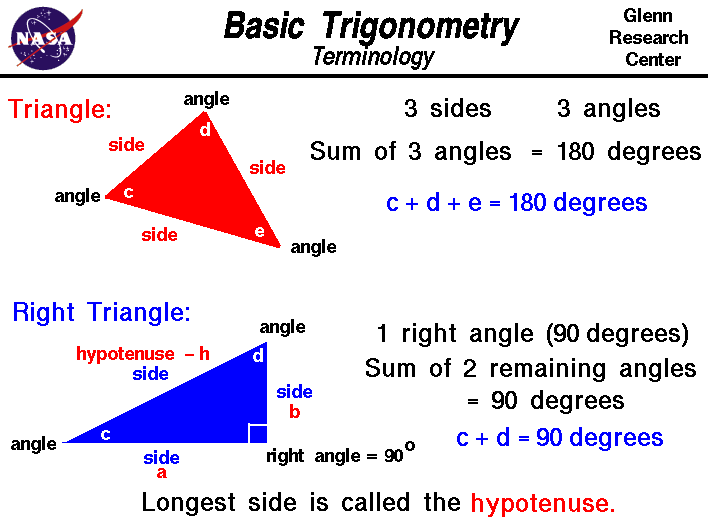
We start with a general triangle. A triangle is a closed shape having
three sides and three internal angles. The sum of the three angles of
any triangle is 180 degrees. If we label the
angles of a triangle c, d, and e, then:
c + d + e = 180 degrees
There are two ways to measure the angles inside a triangle. One way is to measure
the angle in degrees, where 360 degrees equals a complete circle. The
other way is measure the angle in radians, where 2 pi radians equals a
complete circle. Therefore;
360 (degrees) = 2 * pi (radians)
1 degree = .01745 radians
1 radian = 57.2957 degrees
A right triangle is a special case of the general triangle with
one of its angles equal to 90 degrees. A 90 degree angle is
called a right angle and that is where the right triangle gets its name.
The right triangle has some special properties which are very useful for solving problems.
The sum of the three angles of a right triangle is equal to 180 degrees and one
of the angles equals 90 degrees. Then the sum of the other two angles is also 90 degrees.
For a right triangle:
c + d = 90 degrees = pi/2 radians
The important factor here is that if we know (or measure) one angle of a right triangle,we automatically know the value of the other angle.
If we know the value of d, then
c = 90 - d
To describe a triangle in general, we need to know the value of two angles; for a right
triangle we only need to know (or measure) one angle.
Another important piece of information relates
the size of the sides of a right triangle.
We call the side of the right triangle opposite from the right angle
the hypotenuse. It is the longest side of the three sides
of the right triangle. The word "hypotenuse" comes from two Greek words
meaning "to stretch", since this is the longest side.
We will label the hypotenuse with the symbol h and
we will label the other two sides a and b.
Regardless of the size of the hypotenuse, the
ratio
of the size of side a to the hypotenuse h depends
only
on the size of the angle between the side and the hypotenuse.
The value of the ratio is a
function
of the angle and is given the name
cosine of the angle.
On the figure,
cos(c) = a / h
Because of the relations of the angles of a right triangle, we can define
another function of the angle, called the
sine of the angle, which relates side b and
the hypotenuse:
sin(c) = b / h
The key point here is that if we measure one angle, we know the value of all
three angles in a right triangle. And if we additionally measure one side,
we can use these trigonometric functions to determine the length
of all three sides. We can determine 5 pieces of information (2 angles and
3 sides) by making only two measurements.
An additional relation exists between the sides of a right triangle.
If we draw a square on the hypotenuse, and a square on each of the two sides,
the area of the square on the hypotenuse is equal to the sum of the
squares on the sides. This is called the
Pythagorean Theorem
and has been know since ancient times:
h^2 = a^2 + b^2
The Pythagorean Theorem can be used with the trigonometric functions
to determine the size of all the sides of a right triangle.
Activities:
Guided Tours
Navigation ..



- Beginner's Guide Home Page
|
