Most modern passenger and military aircraft are powered by
gas turbine engines, which are also called
jet engines. There are several different types
of jet engines, but all jet engines have some partsin common.
All jet engines have a nozzle which
produces the thrust as described on the
thrust equation slide. The nozzle also
sets the total mass flow rate through the
engine as described on a separate slide.
The nozzle sits downstream of the power
turbine and, while the nozzle does no work on the flow, there are
some important design features of the nozzle.
Because the nozzle does
no thermodynamic work, the total temperature Tt through the nozzle is
constant.
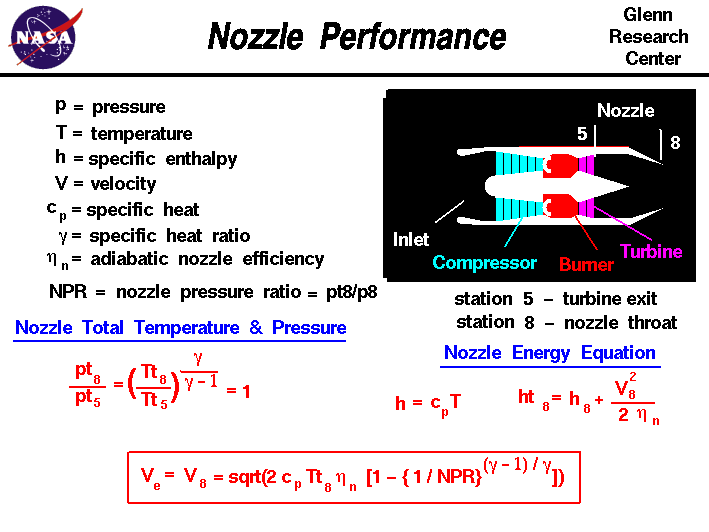
Referring to our station
numbering, the nozzle entrance is station 5 and the nozzle exit
is station 8.
Tt8 divided by Tt5 is 1.0
Tt8 / Tt5 = 1
The total pressure pt across the nozzle is constant as well:
pt8 / pt5 = 1
The static
pressure at the exit of the nozzle is equal to free stream static
pressure, unless the exiting flow is expanded to supersonic
conditions. A convergent-divergent nozzle will have supersonic
exit flow, a simple convergent nozzle will not. The ratio of the
nozzle total to static pressure ratio is called the nozzle
pressure ratio NPR.
NPR = pt8 / p8 = pt8 / p0
Considering the energy equation for
the nozzle, the specific
total enthalpy ht
is equal to the static
enthalpy plus the square of the exit velocity divided by two.
ht8 = h8 + V8 ^2 / 2 / nn
An efficiency factor nn has been included here to account for all the
losses in the nozzle, but its value is normally very near 1.0. With a
little algebra which you learned in middle school, and using the
definitions shown on the slide, you can solve the energy equation for
the exit velocity Ve = V8:
V8 = sqrt(2 * nn * cp * Tt8 * [1 - (1 / NPR)^((gam -1 ) / gam)] )
Using this
velocity, and the mass flow rate through the engine, we can solve the
thrust equation for the amount of thrust
produced by the nozzle.
As shown on this slide, the exit velocity depends on the nozzle
pressure ratio and the nozzle total temperature. The nozzle pressure
ratio depends on the exit static pressure and the
nozzle total pressure. We can determine the nozzle total pressure
from the free stream conditions and the engine
pressure ratio, EPR. EPR depends on the pressure ratio of all
the other engine components. We can also determine the nozzle total
temperature from the engine temperature ratio
, ETR. ETR depends on the temperature ratio of all the other
engine components. With this information, we can solve for the
thrust developed by a jet engine.
The nozzle performance equations work just as well for rocket
engines except that rocket nozzles always expand the flow to some
supersonic exit velocity. You can explore the design and operation of
turbojet and rocket nozzles with our interactive
nozzle simulator program which runs on your browser.
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
