One can calculate the
weight
of any object by multiplying the
density
of the material by the volume of the object.
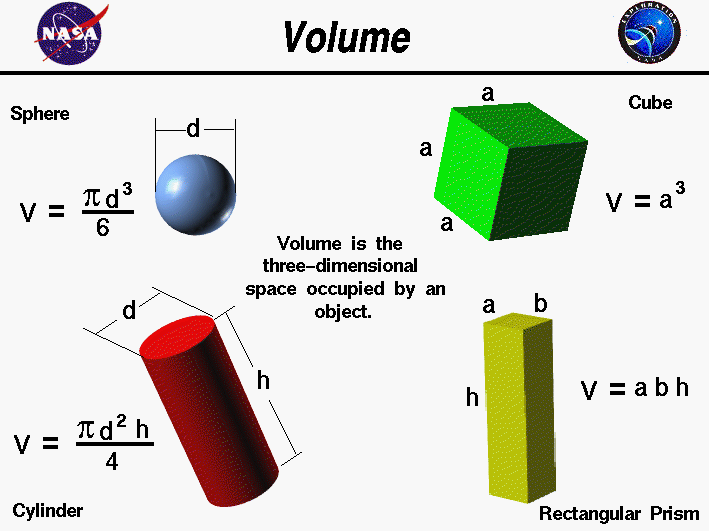
The volume of an object is the three-dimensional space that is
occupied by the object and we are taught
formulas for computing the volume of some simple three-dimensional
objects in middle school. On this slide, we list some equations for
computing the volume of objects which often occur in
aerospace. There are similar equations
for computing the
area
of objects.
The magnitude of the
aerodynamic forces
depends on the surface area of an object, while the
gravitational force
and certain
thermodynamic effects
depend on the volume of the object.
The equations to compute area and volume are used every day by
design engineers.
A simple check on any formula for area or volume
is a dimensional check.
Area is the two-dimensional amount of space that an object occupies.
Area is measured along the surface of an object and has dimensions of
length squared; for example, square feet of material, or square centimeters.
Volume is the three-dimensional amount of space that an object occupies.
Volume has dimensions of
length cubed; for example, cubic feet of material, or cubic centimeters (cc's).
For a sphere, the distance from one point on the surface to another
point on the surface measured through the center of the sphere is called the
diameter.
The volume V of a sphere is equal to pi (3.14159) times the diameter d
cubed divided by six;
V = pi * d^3 / 6
Since the diameter is twice the radius r of the sphere, this equation
can also be written as:
V = pi * 4 * r^3 / 3
For a circular cylinder, we need to know the length h
of the cylinder and the diameter d of the circular cross section.
Then the equation for the
volume is pi times the diameter squared times the length divided
by four;
V = pi * d^2 * h / 4
For a rectangular prism with dimensions a, b,
and h the volume is the product of the three lengths;
V = a * b * h
A cube is a special case of a rectangular prism in which all the sides
are equal to a. The volume equation then becomes;
V = a^3
Here are some special volume equations which are used for rocket nose cones:
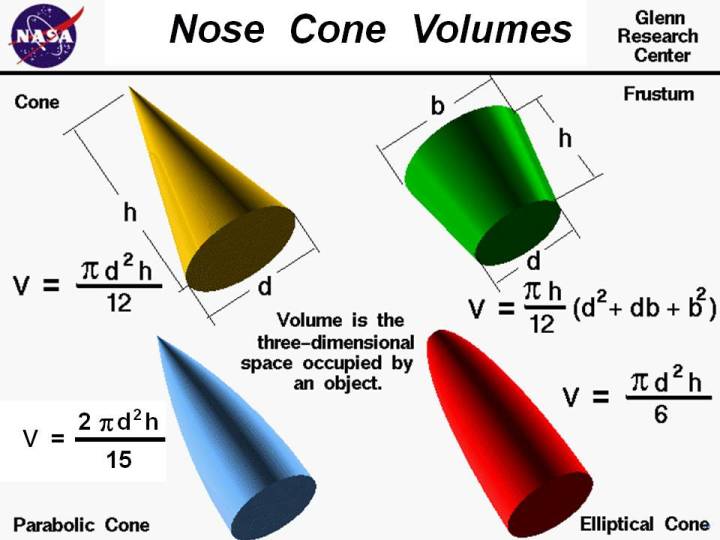
For a cone, the distance from the tip to the base is called the
height. The base is a circle of diameter d.
The volume V of a cone is equal to pi (3.14159) times the diameter d
squared times the height h divided by twelve;
V = pi * d^2 * h / 12
A parabolic cone has a smooth curved surface and a sharp pointed nose.
On the standard cone there is an
edge between the nose and the cylinder which forms the body of
the rocket. But on the parabolic cone,
the surface comes into the base with a slope equal to zero. There is
no edge between the parabolic nose cone and the cylindrical rocket body .
The equation for the
volume is two times pi times the diameter d squared times the height h divided
by fifteen;
V = 2 * pi * d^2 * h / 15
An elliptical cone is similar to the parabolic cone except the
nose is blunted and not sharp. If the nose cone were cut in half, perpendicular
to the base, the resulting cross-section would be half of an ellipse.
The equation for the
volume is pi times the diameter d squared times the height h divided
by six;
V = pi * d^2 * h / 6
The frustum of a cone is formed if the tip is cut off parallel to the base.
Frustum shapes occur often on model rockets as fairings between cylindrical
sections of the body.
The equation for the
volume is pi times the height h divided by twelve times the
quantity: base diameter b squared plus base diameter times cut diameter d
plus cut diameter squared:
V = (pi * h / 12) * (d^2 + d*b + b^2)
Notice: On all of the shapes that have curved (circular) surfaces, we are using the diameter of the
circle in the derivation of the volume. We are not using the radius that is often used in mathematics
text books. The reason for this choice is that
most standard engineering measurements are based on diameter, not radius. It is easier to accurately measure
the diameter of a circular object than to measure the radius. To use the radius, you need to determine where
the center of the circle lies. For a tube, there is no material along the center of the circle. For a sphere,
the center cannot be reached since it is inside the body. You can convert from diameter to radius
(radius = diameter / 2).
Guided Tours
Activities:
Related Sites:
Rocket Index
Rocket Home
Beginner's Guide Home
|
