When two solid objects interact in a mechanical process, forces
are transmitted, or applied, at the point of contact. But when a
solid object interacts with a fluid, things are more difficult to
describe because the fluid can change its shape. For a solid body
immersed in a fluid, the "point of contact" is every point on the
surface of the body. The fluid can flow around the body and maintain
physical contact at all points. The transmission, or application, of
mechanical forces between a solid body and a fluid occurs at every
point on the surface of the body. And the transmission occurs through
the fluid pressure.
Net Mechanical Force in A Static Fluid
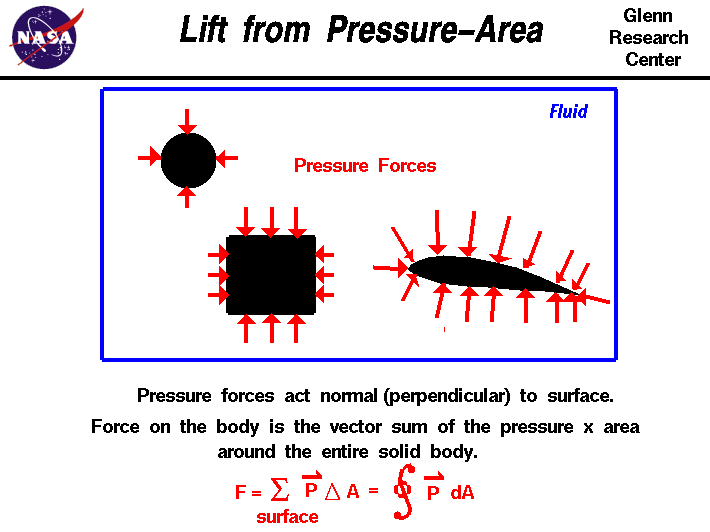
Pressure acts perpendicular to the surface of an object. To obtain
the net mechanical force on the solid object, we have to multiply the
pressure (perpendicular to the surface) times the area around the
entire body. We also have to keep track of the direction of the
pressure times the area. Consider each of the shapes discussed
below:
- Square box. As shown in the figure, for a square box
immersed in a static fluid, the pressure times the area on one
side of the box is balanced by the pressure times the area on the
other side, because the direction of the pressure force is
different. The same is true for the top and bottom of the box. In
a static fluid, there are no mechanical fluid forces on the
surface of a box. (There would be buoyancy forces if the density
of the solid were different from the fluid, but we are neglecting
these effects for now and considering only the mechanical
forces.)
- Cylinder. There are also no net mechanical forces on a
cylinder in a static fluid. The pressure times area forces are all
perpendicular to the surface and, therefore, pass through the
center of the cylinder and cancel each other out.
- Airfoil. As for an airfoil in a static fluid, the
pressure is a constant all around the airfoil. For the simple,
closed surface around the airfoil, the normal (perpendicular)
component of the pressure times the area will cancel out.
In fact, for any simple closed contour, the normal
component of the pressure times the area will sum to zero--no net
force. Since the pressure is constant, we can also conclude that the
sum of the normals to the surface, summed all around a simple closed
surface, will be zero.
Net Mechanical Force in A Moving Fluid
BUT,... if the fluid is not static, but is in motion, the
pressure varies around the closed surface. And the sum of the
pressure (perpendicular to the surface) times the area around the
body produces a net force. Since the fluid is in motion, we can
define a flow direction along the motion. The component of the net
force perpendicular to the flow direction is the lift.
The component of the net force along the flow direction is the
drag. These are definitions. In reality, there is only a
single, net, integrated force caused by the pressure variations along
a body. We can calculate the force on the body by using the equation
at the bottom of the slide. We can break the surface up into a large
number of small areas and sum up the pressure times the area around
the whole surface. In the limit of infinitely small areas, this gives
the integral of the pressure times the area around the closed
surface.
Pressure Variances in A Moving Fluid
How does the pressure vary around a body if the fluid is in
motion? In a fluid, the local pressure is related to the local
velocity. If the velocity changes with location, the pressure changes
as well. If the velocity is low, and no energy is added to the flow,
the relation between pressure and velocity is given by Bernoulli's
equation along a streamline. For an
ideal fluid, with no boundary layers, the surface of an object is a
streamline. If boundary layers are present, things are a little more
confusing, since the external flow responds to the edge of the
boundary layer. And the pressure on the surface is imposed from the
edge of the boundary layer. If the boundary layer separates from the
surface, it gets even more confusing.
Summary
So, to summarize, for any object immersed in a fluid, the
mechanical forces are transmitted at every point on the surface of
the body. The forces are transmitted through the pressure, which acts
perpendicular to the surface. The net force can be found by
integrating (or summing) the pressure times the area around the
entire surface. For a moving flow, the pressure will vary from point
to point because the velocity varies from point to point. For some
simple flow problems, we can determine the pressure distribution (and
the net force) if we know the velocity distribution by using
Bernoulli's equation.
But, how do we determine the velocity distribution around a body?
Specifying the velocity is the source of error in two of the more
popular incorrect theories of lift.
What causes the velocity to change around a body? This leads us to
an alternate way of looking at fluid forces involving
the Navier-Stokes Equations .
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
