Ramjets,
scramjets,
and
rockets all use
nozzles
to accelerate hot exhaust to produce
thrust as described by
Newton's third law
of motion. The amount of thrust
produced by the engine depends on the
mass flow rate through the engine, the exit velocity
of the flow, and the pressure at the exit of the engine. The value of these
three flow variables are all determined by the nozzle design.
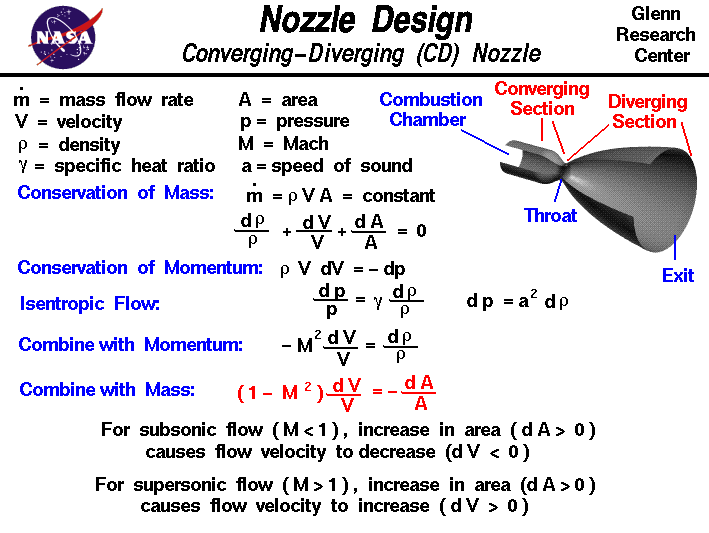
A nozzle is a relatively simple device, just a specially shaped
tube through which hot gases flow. Ramjets and rockets typically
use a fixed convergent section followed by a fixed divergent section
for the design of the nozzle. This nozzle configuration
is called a convergent-divergent, or CD, nozzle.
In a CD nozzle, the hot exhaust leaves the combustion chamber
and converges down to the minimum area,
or throat, of the nozzle. The throat size is chosen to
choke the flow and
set the mass flow rate
through the system.
The flow in the throat is sonic which means the
Mach number
is equal to one in the throat. Downstream of the throat,
the geometry diverges and the flow is
isentropically
expanded to a supersonic Mach number that depends on the
area ratio
of the exit to the throat.
The expansion of a supersonic flow causes the static pressure and temperature to
decrease from the throat to the exit, so
the amount of the expansion also determines the exit pressure and
temperature.
The exit temperature determines the exit
speed of sound, which determines the
exit velocity.
The exit velocity, pressure, and mass flow through the nozzle determines
the amount of thrust produced by the nozzle.
On this slide we derive the equations which explain and describe why
a supersonic flow accelerates in the divergent section of the nozzle
while a subsonic flow decelerates in a divergent duct. We begin with the
conservation of mass equation:
mdot = r * V * A = constant
where mdot is the mass flow rate, r is the gas
density, V is the gas velocity,
and A is the cross-sectional flow area. If we differentiate
this equation, we obtain:
V * A * dr + r * A * dV + r * V * dA = 0
divide by (r * V * A) to get:
dr / r + dV / V + dA / A = 0
Now we use the
conservation of momentum equation:
r * V * dV = - dp
and an
isentropic flow relation:
dp / p = gam * dr / r
where gam is the
ratio of specific heats.
This is Equation #10 on the page which contains the
derivation
of the isentropic flow relations
We can use algebra on this equation to obtain:
dp = gam * p / r * dr
and use the
equation of state
p / r = R * T
where R is the gas constant and T is temperature, to get:
dp = gam * R * T * dr
gam * R * T is the square of the
speed of sound a:
dp = (a^2) * dr
Combining this equation for the change in pressure with the momentum equation
we obtain:
r * V * dV = - (a^2) * dr
V / (a^2) * dV = - dr / r
- (M^2) * dV / V = dr / r
using the definition of the
Mach number M = V / a.
Now we substitute this value of (dr /r) into the mass flow equation to get:
- (M^2) * dV / V + dV / V + dA / A = 0
(1 - M^2) * dV / V = - dA / A
This equation tells us how the velocity V changes when the area A
changes, and the results depend on the Mach number M of the flow.
If the flow is subsonic then (M < 1) and the term multiplying the
velocity change is positive (1 - M^2 > 0). An increase in the area
(dA > 0 ) produces a negative increase (decrease) in the velocity (dV < 0).
For our CD nozzle, if the flow in the throat is subsonic, the flow downstream
of the throat will decelerate and stay subsonic. So if the converging section
is too large and does not choke the flow in the throat, the exit velocity
is very slow and doesn't produce much thrust. On the other hand, if the
converging section is small enough so that the flow chokes in the throat,
then a slight increase in area causes the flow to go supersonic. For a
supersonic flow (M > 1) the term multiplying velocity change is negative
(1 - M^2 < 0). Then an increase in the area (dA > 0) produces an increase
in the velocity (dV > 0). This effect is exactly the opposite of what happens
subsonically. Why the big difference? Because, to conserve mass in
a supersonic (compressible) flow,
both the density and the velocity are changing as we change the area.
For subsonic (incompressible) flows, the density
remains fairly constant,
so the increase in area produces only a
change in velocity. But in supersonic flows, there are
two changes; the velocity and the density. The equation:
- (M^2) * dV / V = dr / r
tells us that for M > 1, the change in density is much greater than
the change in velocity. To conserve both mass and momentum in a supersonic
flow, the velocity increases and the density decreases as the area is
increased.
Activities:
Guided Tours
Navigation ..


- Beginner's Guide Home Page
|
