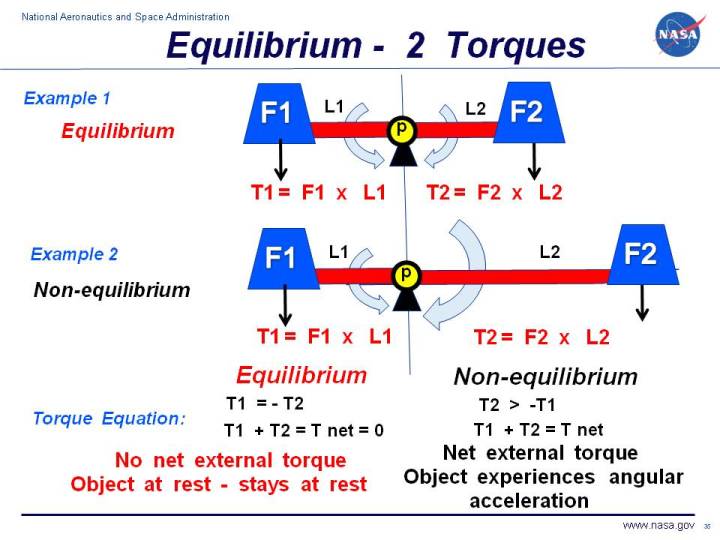
A very basic concept when dealing with
torques
is the idea of equilibrium or balance.
In general, an object can be acted on by several torques
at the same time.
A torque is a
vector quantity
which means
that it has both a magnitude (size) and a direction associated with it.
If the size and direction of the torques acting on an object are
exactly balanced, then there is no net torque acting on the object
and the object is said to be in equilibrium.
Because there is no net torque acting on an object in equilibrium,
an object at rest will stay at rest, and an object in constant angular motion
will stay in angular motion.
Let us start with the simplest example of two torques acting on an object.
In Example 1 on the slide, we show a red bar, or arm, on which two blue
weights are placed at either end. There is a pivot point, labeled p which
is located in the exact center of the bar, breaking the bar into two equal lengths L1
and L2. The weights F1 and F2 are also of equal size.
The weight F1 and arm L1 generate a
torque T1 about the pivot point in the
counter-clockwise direction.
Similarly, the weight F2 and arm L2 generate a torque T2,
but this torque is in the clockwise direction. Remember that
torques are vector quantities and direction is important.
Two torques with the same magnitude but different directions
are not equal torques. In fact,
T1 = - T2
If we sum up the torqes acting on the pivot p,
we obtain the torque equation on the left:
T1 + T2 = T net = 0
where T net is the net torque acting on the pivot.
Because the net torque is equal to zero, the torques in Example 1 are balanced and
acting in equilibrium.
There is no net torque acting on the pivot in Example 1. Since the system is initially at rest
(angular velocity equals zero), the system will remain at rest.
If the system was rotating with a uniform
angular velocity,
it would continue rotating
at the same angular velocity.
In Example 2, we have increased the length of the arm L2 so that it is much
greater than arm L1. The torque T2 is then larger than the torque
T1. The torques are no longer in equilibrium.
The torque equation remains the same, but the net torque is not equal to zero.
The magnitude of the net torque is given by:
|T net| = |T1| - |T2|
where the "| |" symbols indicate the magnitude of the quantity included between the ends.
The direction of the net torque would be in the clockwise direction because T1
is less then T2.
If the system were initially at rest, the system would begin to
accelerate clockwise.
Because there is a net torque in
Example 2, the torques are not in equilibrium.
Because the system is pinned at point p, the system will rotate clockwise until the
long arm is located directly beneath the pivot and the short arm is directly above the pivot.
If angular momentum carries the system past this point, then the sense of the rotation will
change and the system will rotate counter-clockwise. If there is some friction in the pivot,
the system will eventually come to rest with the long arm L2 directly below the pivot.
At that time, there is no net torque about the pivot and the system will again be in equilibrium.
Navigation..



- Beginner's Guide Home Page
|
